Home »
Misc »
How does friction and gravity affect basketball
How does friction and gravity affect basketball
The physics of basketball and bracketology
The March Madness craze begins soon. People have already started creating brackets to figure out who will be the best team in college basketball. With all this basketball on people’s minds, it’s a good time to look at some of the physics, math, and art behind the most exciting sport in March.
The Ball
The first and most important element of the entire sport is the basketball. The ball hasn’t always been the bumpy ball we use today. When teams first started playing, things like soccer balls were used. If you picture a soccer ball, you realize it’s far smoother than a basketball.
Players had trouble dribbling or passing the ball because it would slip out of their hands. So the ball was made bigger, and bumps were added to make the ball easier to hold on to. The bumps cause more friction between the ball and the player’s hands, and the friction makes the ball easier to handle. With bumps added to the basketball, actions such as dribbling and passing are easier.![]()
Both of these actions have elements of physics.
The Dribble
The simple act of dribbling the ball highlights each of Newton’s three laws. When you start to dribble:
- You and gravity both apply force on the ball.
- The ball accelerates toward the ground with the force of gravity.
- After the ball hits the ground, an equal but opposite amount of force acts on the ball, forcing it back up into your hand.
The more force applied to the ball at the beginning of the dribble, the higher the bounce. The height of the bounce is also affected by the surface being dribbled on and the air inside the ball. If the surface is denser, less force is transferred away from the ball, and the ball bounces higher. The most common basketball surface in a gym is maple wood because it has a high density rating and high shock resistance, which helps with bouncing and athlete safety when jumping. The ball has far less bounce on a soft surface such as carpet.
The air inside the ball helps with the transfer of energy.
When the ball hits the ground, the air inside is compressed. The energy in the compressed air pushes back in the opposite direction of the force and causes the ball to bounce. This is why a ball with less air won’t bounce as well.
The Pass
When passing the ball, players must always compensate for gravity. You normally aim to pass the ball to someone at chest level. If you try to pass a ball straight to someone’s chest, you will probably hit them lower than intended. This is because gravity is constantly forcing the ball toward the ground. To compensate for gravity, the trajectory of a pass is usually above the intended target.
The Shot
The same compensation for gravity is present when you shoot the ball. With the basket positioned 10 feet off the ground, a straight shot won’t ever make it into the hoop. When shooting a basket, you apply an upward force to the ball and gravity brings the ball back down. The initial force you apply to the ball along with the force of gravity is what gives your basketball shot that pretty arc similar to a parabola.
Every shot in basketball is a little taste of geometry, and the best shot that applies a little bit of geometry ends with an always-satisfying swish.
The Bracket
So, we can’t talk spring ball without including the infamous March tournament bracket.
Some might say picking the right outcomes in the bracket is an art. Others might contend it’s a science and that you can apply engineering and statistics to selecting your top teams. One example is the University of Illinois’ analytics-based approach.
With a little creativity, you could even use basketball to test some physics lessons in class. A simple activity could be to vary air pressure in a basketball and test its effect on the bounce of the ball.
Or check out these ideas:
- “How to Incorporate March Madness into Your Classroom”
- “March Madness: Using Tournament Brackets to Debate Academic Questions”
- "Basketball Science: Hooking March Madness Fever to Hands-on Sports Science Experiments”
With a little imagination, you could easily turn the hype around basketball during March into an exciting hands-on STEM education experience for students!
TOPICS: IN THE CLASSROOM, IDEAS & INSPIRATION, Science, STEM, Engineering
Forces - The Physics of Basketball
Forces A force is a quantity measured in Newtons (N) and occurs whenever there is an interaction between objects and/or people.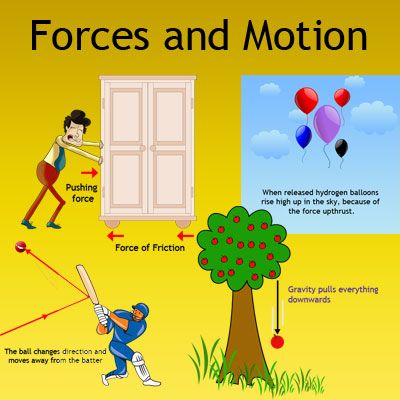
There are different kinds of forces, which include: frictional, tension, normal, air resistance, applied, and spring. These are all forces that occur when there is physical contact. Forces that don’t require physical contact include: gravitational, electrical and magnetic.
In basketball, there are many kinds of forces occurring everywhere.
Frictional: -Allows player to run, jump, move side to side, etc. on the court without sliding (sole of shoe grips the hardwood floor)
-Allows a player to grip the ball in order to dribble, shoot, pass, etc.
Tension: -Tied up laces on basketball shoes allow for increased security around the ankle
-When the ball goes through the net, tension in the mesh of the net absorb the impact of the ball to slow down its movement
Normal: -Keeps objects (i.e. players, ball, net, from entering the floor), as it is perpendicular to the surface of contact (i.
e. hardwood basketball court)
Air Resistance: -Helps to slow down the speed of moving objects i.e player running, ball being passed, etc.
Applied: -Allows player to dribble, shoot, pass, block, etc. with a regulated force
-Allows player to resist other external forces acting on it (i.e. gravity, frictional, tension, air resistance, etc.)
Spring: -Some basketball shoes may contain springs in the bottom to allow better shock absorption due to contact
-Spring in bottom of basketball shoe may allow player to jump higher and move faster
Gravitational: -Allows objects to fall back to the ground when launched in air (i.e. shooting or passing ball)
-Allows people to move and jump without floating off; ensures things will come back to the contact surface
Newton's Laws of Motion:
Isaac Newton Newton created the three laws of motion.
Movements in basketball can occur due to these laws. They include:
1. Every object in a state of uniform motion remains in that state of motion unless an external force is applied to it.
2. The relationship between an object's mass, its acceleration, and the applied force is F=m*a; direction of the force is proportional to the direction of the acceleration.
3. For every action there is an equal and opposite reaction.
Forces of Dribbling a BasketballThe video above shows the most basic technique of dribbling a basketball (in reality, this would be a double dribble violation because he picks the ball up with two hands then continues to dribble again, however for the purpose of this analysis, focus primarily on the ball being forced downward and how it bounces back up).
Types of Forces: The boy can grip and move the ball in control because of friction and how the ball is designed to have channels (black grooves) in order to provide a more stable grip.
He applies a force downward and the ball falls to the ground with the help of gravity. When the ball is only in the air, only the force of gravity is acting on it. When it hits the ground, the normal force keeps it from sinking into the ground. (The free body diagrams below express the various forces)
Newton’s First Law: When the boy is simply holding the ball in his hands there is a balanced force which prevents the ball from moving. According to Newton’s first law of motion, the only reason why the ball stops accelerating downward is because of the external force of the ground acting on it in the other direction. This external force enables the ball to then accelerate upward back into the boy’s hand, which acts as another external force that stops the ball from accelerating. Without this law the ball would continue to accelerate uncontrollably when acted on by an applied force.
Newton’s Second Law: Acceleration of the ball being dribbled is determined by the amount of force applied on it.
Since the ball has a mass, the boy had to apply a great enough force in order to create an unbalanced force and overcome external forces resisting it from moving. If he wanted to dribble the ball in a different direction, he must apply that force in that direction. If he wanted to dribble slower he would apply a less amount of force. The force applied on the ball by the boy and the force the ground applied on the ball can be expressed using the equation: F=m*a. Good basketball players know how to regulate how much force is needed to complete a skill effectively. The calculations below describe the amount of force that the boy applied on the ball in order for it to accelerate downward onto the ground.
Newton’s Third Law: Action and reaction forces occur when the boy’s hand starts to apply a downward force on the ball. As his hand is pushing downward (action force) ball is applying an equal force upward on his hand (reaction force). When the ball applies a force to the ground (action force), the ground applies an equal force upward onto it (reaction force), which allows the ball to bounce back upward.
Why does the ball move along "incredible" trajectories in some sports? • Yuri Erin • News of science on "Elements" • Physics
In team sports, it is common to see the ball move in the air along a highly curved path, causing surprise not only for the players, but also for the spectators. French scientists conducted a series of experiments to study the movement of rotating balls in water and, based on the data obtained, built a theoretical model of their behavior. With the help of the developed model, scientists answered the question in which sports the ball can fly in a steep arc.
More and more often various phenomena from the field of sports become the object of research by physicists. The most attractive from a scientific point of view are sports with a ball. The fact is that due to air resistance, the movement of the ball turns out to be a non-linear process as a whole, and therefore, despite the seeming routine, it is of great interest for theoretical and experimental study.
The non-linearity of the ball's behavior can be observed, for example, during the broadcast of football matches, when commentators reward the trajectory of its flight with epithets like "fantastic", "incredible", "crazy", etc. One of the most striking and well-known examples of such an "incredible » trajectory - Brazilian footballer Roberto Carlos' free kick (see video), which he delivered on June 3, 1997 years on the gates of the French team. When watching the video, the viewer may initially think that the ball flies far to the right of the goal, but then the direction of his path is sharply curved, and he, to the amazement of the French goalkeeper, flies into the right corner of the goal. The influence of the wind is absolutely excluded here, since at that moment the weather was calm.
So there is nothing surprising in the fact that this flight of the ball has become the subject of a comprehensive study of scientists (see, for example, the article "Football Physics" in the journal "Technology of Youth").
At a qualitative level, the cause of the ball moving in a steep arc is known - it is the force that arises due to the rotation of the ball, which is often called the Magnus force. But, despite repeated attempts, no adequate theoretical model has been created that could correctly quantify to interpret the flight of the ball.
This omission was recently corrected by a group of French scientists. In their article The spinning ball spiral, published in New Journal of Physics , they not only modeled the goal of Roberto Carlos on a quantitative level, but also showed in which sports the movement of the ball can have the same "fantastic" trajectory.
To begin with, the authors of the article, after conducting a series of experiments, studied the trajectories of rotating polypropylene and polyformaldehyde balls with a radius of several millimeters, which were fired into the aquatic environment using a special slingshot. The design of the slingshot allowed the balls to be given controlled values of rotation and speed, as well as a specific angle at which they had to hit the liquid.
The choice of water and polypropylene or polyformaldehyde is due to the fact that the densities of these substances are very close to each other. Therefore, it is possible to simplify the task and not take into account the influence of gravity on the parameters of the movement of the balls. The motion trajectory of the studied objects was detected by a high-speed video camera.
Visualization of one of the experiments can be seen in fig. 1. It shows a series of freeze-frames showing the position of a spinning polypropylene ball in water.
It can be seen with the naked eye that the ball moves in a spiral, and we note that in the first four photographs its trajectory is similar to the flight of the ball launched by Roberto Carlos.
Thus, the experiment gave an already obvious conclusion that the reason for the curvilinear motion of the ball lies in its rotation. Now it was up to building a neat theoretical model of the dynamics of balls in water.
In the process of motion, two forces act on the object under study — the drag force, which under given conditions is proportional to the square of the ball's speed, and the Magnus force, which is proportional to the product of the ball's speed and the angular speed of its rotation.
To take them into account, it is necessary to know exactly the value of the proportionality coefficients included in the formulas for both forces. Their values depend on the geometry of the body, as well as on how much the body disturbs the environment with its movement. This perturbation in hydro- and aerodynamics is characterized by a dimensionless quantity - the Reynolds number. The larger the Reynolds number, the stronger the medium is perturbed under the action of a moving body. For given ranges of values of the Reynolds number, there is a proportionality factor in the formulas for forces. Fortunately, for spherical bodies, the values of these coefficients depending on the Reynolds number were measured, so the authors used ready-made experimental data.
Another difficulty that the scientists successfully overcame was purely mathematical. If you try to write the equations of motion (Newton's second law) in the traditional Cartesian coordinate system, then because of their form they will not have an analytical solution.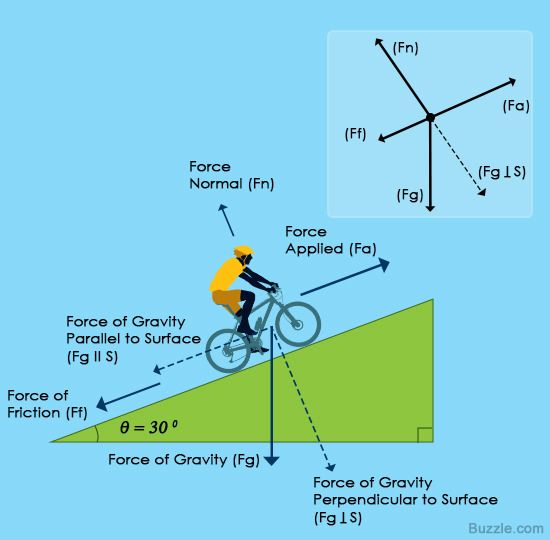
Of course, you can use existing programs for numerical calculation, but then you lose "visibility" in understanding the ongoing process, more precisely, how the parameters of the ball (rotation speed, radius, density) and the medium will affect the trajectory of motion. Since the experiments clearly demonstrated the spiral trajectory of the sphere, the authors used the equations of motion written in a special curvilinear coordinate system, sometimes called the Frenet-Serret coordinate system.
Thanks to this mathematical "trick", the equations can be solved analytically, and, accordingly, there is no need to resort to any numerical calculation. Further, using the known relations between the Frenet-Serret and Cartesian coordinate systems, the authors of the article plotted solutions to the equations of motion, which, in fact, determine the trajectory of a rotating ball in water (Fig. 2). As can be seen from fig. 2, the movement of the rotating ball is in a spiral. The red spiral corresponds to the case when the rotation speed of the polypropylene (polyformaldehyde) ball remains constant during movement.
It is obvious that such a picture has little in common with reality. If we now take into account the fact of a decrease in the angular velocity of rotation (a realistic situation), then the path of the object under study will pass along a blue spiral, which, as can be seen, is in excellent agreement with the experimental data.
Ultimately, as the analysis of the expression describing the trajectory of the ball showed, its path becomes straight. The distance at which the ball trajectory is bent is approximately equal to the value designated by the authors as (this can also be seen from the graph in Fig. 2). This parameter, which the authors also called the "characteristic scale of the spiral", is determined through the radius of the ball, the ratio of the densities of the substance of the ball and the medium, and the coefficient of proportionality included in the formula for drag. is a very important parameter, which will be discussed below.
So, the authors of the article have created an adequate quantitative theory of the motion of a rotating ball in water, which is in perfect agreement with the experiment.
However, since at the very beginning of this note we were talking about the flight of the ball, the question arises as to the applicability of the model described here in conditions where the influence of gravity can no longer be neglected, and the aquatic environment changes to air. How much can gravity distort the helical flight path of a ball spinning in the air?
To answer these questions, the authors provide a table in which they have collected the main parameters of sports games with the ball. Using the given values, the authors calculated the characteristic scale of the spiral along which the ball would move in the absence of gravity (the same), and the characteristic distance (scale) of the action of gravity U 0 2 /g, after which the ball's trajectory is determined mainly by gravity.
Comparison of the last two columns of the table allows us to determine which sports are dominated by aerodynamics (which is precisely reflected in the spiral trajectory of a rotating ball), and in which by gravity.
It can be seen that in table tennis, golf and tennis, the scale of gravity is several times smaller - therefore, in these sports, the rotating ball will move in a spiral. In basketball and handball, the opposite picture takes place: gravity dominates here, which means that the movement of a spinning ball does not lead to a serious curvature of the trajectory. Finally, there is a category of sports in which the effects of aerodynamics and gravity are approximately the same - these are football, baseball and volleyball.
Football deserves special attention in this list. For him, the characteristic scale of the spiral (= 54 m) is two times smaller than the characteristic scale of the action of gravity. This means that the motion of a spinning ball will deviate substantially from a straight line only when it has traveled a sufficiently large distance. Only in this case, the trajectory of the ball becomes "incredible".
Returning to the goal of Roberto Carlos, we note that the distance to the goal of the French team during the execution of the free kick by the Brazil player was approximately 35 meters.
This value, although close to the characteristic scale of the spiral in football, is still less than it. However, since Roberto Carlos not only gave the ball a spin, but also, due to a strong blow, gave it a speed 1.5 times higher than the “usual” maximum value of 30 m / s indicated in the table, the scale of gravity has increased more than twice, and gravity began to have a much smaller effect on the flight of the ball. This, combined with a large distance to the goal, led to the ball flying into the goal in a steep arc.
Source: Guillaume Dupeux, Anne Le Goff, David Quéré and Christophe Clanet. The spinning ball spiral // New J. Phys. 12, 093004 (2010).
Yuriy Yerin
Influence of playing basketball on the formation and all-round development of schoolchildren’s organism — Secondary School No. 8 of Birobidzhan
morally stable younger generation. Unfortunately, today we are faced with a very serious problem - the general weakening of the health of graduates - schoolchildren.
Most of them are not energetic, physically weak, anemic, suffer from various types of health problems. The bulk of today's students are practically not fond of sports, they are not interested in physical education lessons. The health of 80% of students is weakened, there is a violation of posture, underdevelopment of muscle mass, obesity and dystrophy. The activity of schoolchildren is very low, they are drowsy, they can hardly cope with the curriculum. The psyche of most of them is not stable, the children are quick-tempered, touchy, and react inadequately to comments. These circumstances prompted us to conduct experimental work with the group of schoolchildren who play basketball.
Basketball is an intense sport game, one of the most important means of physical education. Systematic basketball exercises strengthen health, promote comprehensive physical development, and bring up the will, perseverance, and courage. It attracts with its spectacularity, abundance of various technical and tactical techniques, emotionality, airiness, dynamism, collectivism and individualism at the same time, and besides, in our opinion, and many specialists, it is the most effective means for comprehensive physical development.
By the way, basketball is perhaps the only popular sport that has managed to win the hearts of fans all over the world in a matter of decades, which in itself seems to be an unprecedented phenomenon. The popularity of basketball and its widespread use in the system of physical education are determined, first of all, by the economic availability of the game, high emotionality, great spectacular effect, a complex effect on the body and education of young people, and therefore, further in the text, we give the most characteristic features of basketball.
Basketball is based on natural movements - running, jumping, throwing, passing. They are easy to teach children, teenagers and adults. Therefore, basketball is included in the program of upbringing and education of children, starting from kindergartens, and ball games - from the age of two. The desire to surpass the opponent in the speed of actions aimed at achieving victory teaches those involved to mobilize their capabilities, act with maximum effort, and overcome difficulties that arise in the course of wrestling.
These features contribute to the education of perseverance, determination and purposefulness.
A varied alternation of movements and actions, often changing in intensity and duration, has a general complex effect on the body of those involved. Basketball lessons contribute to the development of basic physical qualities. The game environment changes very quickly and creates new game situations. These conditions teach players to constantly monitor the process of the game, instantly assess the situation, act proactively, resourcefully and quickly in any situation. Continuous observation of the game process helps the development of abilities for a wide distribution and concentration of attention, for spatial and temporal orientation.
Basketball is popular all over the world. But the training of young athletes is a time-consuming and responsible business, since mistakes can lead to various adverse health consequences. Therefore, the tasks of training students, means, methods, forms of organization of the educational and training process should, first of all, follow from the age patterns of their development and the functional capabilities of the body.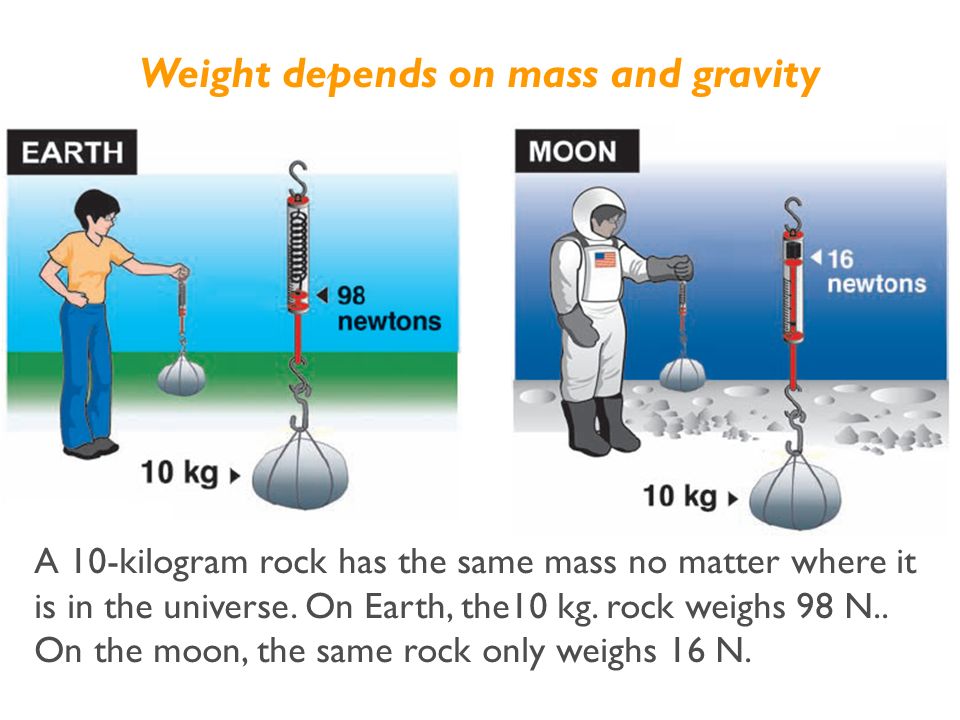
A variety of basketball practice conditions contribute to the comprehensive physical development, especially of such motor qualities as speed, endurance, dexterity, strength. Various game situations, possession of the ball, fighting with an opponent involve large muscle groups and have a positive effect on the development and strengthening of the main functional systems of the body, primarily on the cardiovascular, respiratory and autonomic nervous systems. During training sessions, moral and volitional qualities are brought up in children - discipline, courage, perseverance, the ability to overcome difficulties of any nature, diligence, a sense of collectivism.
A number of features of basketball determines its great health-improving, educational and applied value. The theory and methodology of youth sports take into account the age characteristics of schoolchildren, the specifics of the use of means, methods, organizational forms that are most appropriate for each stage of many years of sports training.![]()
In comparison with other methods and forms of physical education of schoolchildren, sports, and in particular basketball, most effectively stimulates positive functional and morphological changes in the developing organism, to a greater extent affects the development of motor abilities.
It is reasonable to believe that it is sport that most contributes to the mental development of children and adolescents. Teenagers are generally characterized by rapidly developing self-awareness, the desire to experience the valuable qualities of a person (volitional, moral, physical). And it is in sports that schoolchildren find effective means of developing these abilities.
The competitive nature of the game, the continuous change in the situation, success or failure causes athletes to display a variety of feelings and experiences that affect their activities. A high emotional level helps to maintain constant activity and interest in the game. These features of basketball create favorable conditions for educating basketball players, the ability to manage emotions, not to lose control over their actions.![]()
Each player during the meeting, taking into account the changing game environment, not only independently determines what actions he needs to perform, but also decides when and how to act. This is important for educating those involved in creative initiative. In general, we should not forget that of all team sports, basketball is more prone than others to display individual ability and dribbling, and also, at times, single-handedly decide the outcome of this or that match.
The rules of the game provide for the ethical behavior of athletes in relation to opponents and referees. Personal and technical punishments serve as a means to regulate the relationship between the participants in the competition. This feature is most important for fostering friendship and camaraderie, and developing the habit of subordinating one's actions to the interests of the team.
Basketball has become widespread all over the world, every year the interest in this sport increases, the competition in the international arena intensifies.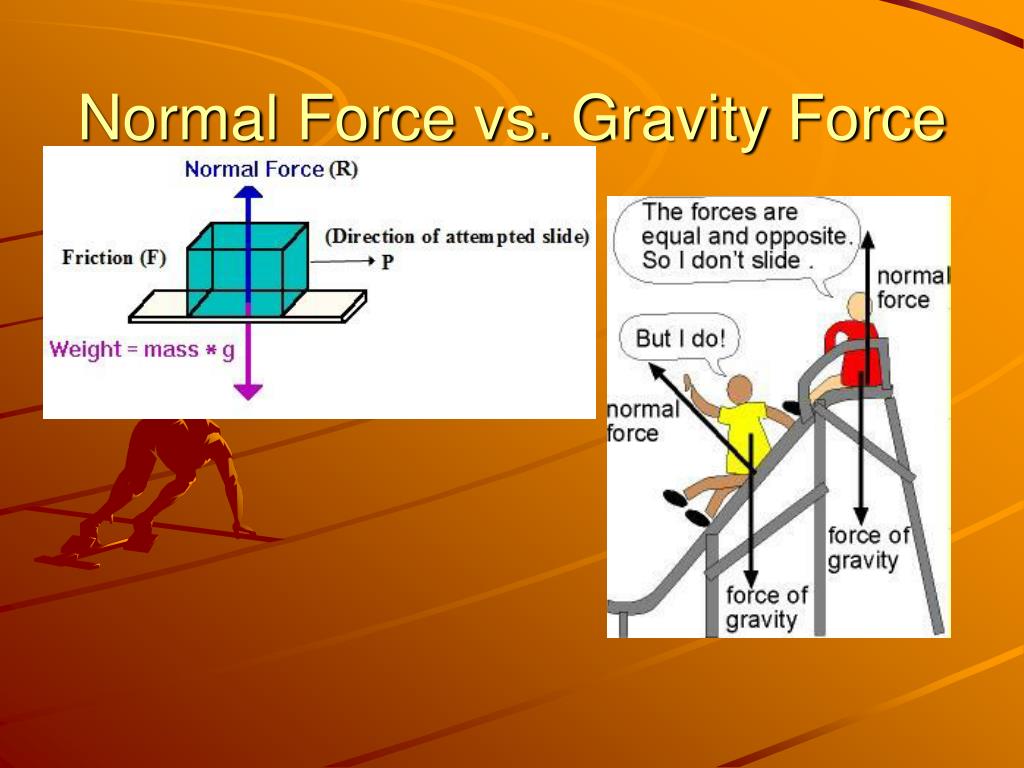
The latter causes the need to improve teaching methods, taking into account the development trends of basketball. The variety of motor actions of athletes during the game makes it very difficult to quantify their components. The modern educational process urgently puts forward the need to develop methods for an integrative qualitative-quantitative description of an athlete's body as a large system in order to rationally model his condition.
In the course of the research, the features of the physical fitness of children involved in basketball were determined, as well as the initial level of development of the physical qualities of children according to six tests presented. Further work took shape in the development and testing of the OFP program for the experimental group with a focus on developing the general physical qualities of young basketball players. The obtained theoretical and practical material confirms our hypothesis that in a general education school the methodology for the development of physical qualities in the classroom under the program with basketball training contributes to an increase in functional performance and general physical training of students.
