Home »
Misc »
How to calculate winning percentage in basketball
How to calculate winning percentage in basketball
Winning Percentage Calculator
Created by Bogna Szyk
Reviewed by Steven Wooding
Last updated: Jun 30, 2022
Table of contents:
- Win percentage formula
- How to calculate winning percentage with ties
- Should you bet on this team?
If you want to know how good the last season really was for your favorite baseball or hockey team, you should definitely give this winning percentage calculator a try. All you have to do is input the number of wins, losses, and ties on the team's record, and you'll have an answer in a split second!
💡 Click on the Advanced mode button under the calculator to include tied games and to assign their value.
Win percentage formula
Calculating the winning percentage is equivalent to estimating a proportion of wins in the total number of games. If there are no tie results, you need to divide the number of wins by the total number of games (wins and losses):
winning percentage = wins / games
For example, let's assume that your favorite basketball team has played 82 games and won 48 of them.![]()
Their winning percentage is:
(48 / 82) × 100 = 58.54%
How to calculate winning percentage with ties
If, on the other hand, you want to include ties into the whole calculation, the formula gets a bit more complicated. It is usually assumed that a tie is worth the same as 1/2 of a win. In such a case, you can calculate the percentage in the following way:
winning percentage = (wins + 0.5 × ties) / games
For this equation, the number of games is the sum of win, loss, and tie results on the team's record.
To get a better understanding of this formula, let's consider the following example: a football team playing in the National Football League has played 16 games in total. They lost 4 of them and got a tie result in 5. What is their winning percentage?
-
Determine the number of wins. If the total number of games is 16, then you can use the formula below:
wins = games - ties - losses = 16 - 5 - 4 = 7
-
Now, you know that the team has won 7 games during the last season.
Add that number to half of the tie results:
wins + 0.5 × ties = 7 + 0.5 × 5 = 9.5
-
Divide the number you got by the total number of games:
(9.5 / 16) × 100 = 59.38%
-
59.38% is the winning percentage of the football team you cheer for. Quite good, but still not enough to win the League!
🙋 We use percentages in almost all aspects of our life, not just sports. For example, we can also use percent to express the relative error between the observed and true values in any measurement. To learn how to do that, check our percent error calculator.
Should you bet on this team?
Even if your favorite team has a stellar track record and a winning percentage oscillating around 80%, it doesn't necessarily mean they will win the next match! Instead of calculating the win percentage, you should use our odds calculator to determine your chances when betting on them.
Bogna Szyk
Losses
Number of games
Winning percentage
Check out 9 similar percentage calculators
Percent offPercent errorConvert fraction to percentage… 6 more
Win Percentage Calculator: Calculate Winning Percentage
You can use the win percentage calculator to find the winning percentage in the presence of three variables: Wins, losses, and draws(ties).
You need only to enter the number of the wins, losses, and ties games in the winning percentage calculator for determining the performance of your favorite team in the last season.
In the topic below we are going to discuss how to calculate winning percentage and the terms related to the win percentage and performance of a team.
How to Calculate Win Percentage?
When we are calculating the winning percentage, there are no tie games. Then we divide the number of games won by the team by the total number of games played by the team. In this, we need to include the number of losses in the total number of games.
The winning percentage= (Number of Games Won /Total Number of Game ) * 100
Where:
Number of Games Won= Number of games won by the team
Total Number of Game = Number of games won + Number of games lost
Well, the most appealing reason behind providing an online Winning percentage calculator is that it works best for finding the average of winning of a team or an individual.
Example:
If your favorite football team has played in a total of 18 matches, It won 13 games and lost 5, then their winning percentage is as follows:
The winning percentage= (13 /18)*100
The winning percentage= 72.22%
Although the above formula is simple to remember, the use of a winning percentage calculator displays the result simply by inputting the values of the number of games played and inserting the values of won and lost games.
Ties and Winning Percentage:
When we are calculating the winning percentage, there are tied games. In this scenario, we add the tied games along with the number of games won plus the number of games lost and games tied.
The winning percentage= (Number of Games Won /Total Number of Game)* 100
Number of Games Won= Number of games won by the team
Total number of games= Number of games won + Number of games lost + Number of ties
You only have to input the number of wins, losses, and draw (ties), the win-loss ratio calculator will find the result in a split of seconds.
Example:A basketball team has played in a total of 22 matches, it won 15 games and lost 2 and tied games are 5, then their percentage calculated the winning percentage calculator are as follows::
The winning percentage= (15/ 22)* 100
The winning percentage= 68.18%
And, if you need to calculate win percentage with ties, then simply add ties along with the number of wins and losses into our win percentage calculator.
When you calculate the performance of a team having Wining, Losses, and draws(ties), we need to use the Win percentage calculator with ties to find the performance of our favorite team.
Table of percentage Winning:
In the following table, we are only adding the Win and losses against the number of total games played. Add the values in the win calculator for finding the output values. We are not adding the ties games in the table below:
| Win | Losses | % age |
| 5 | 4 | 55. 56 |
| 4 | 5 | 44.44 |
| 3 | 6 | 33.33 |
| 2 | 7 | 22.22 |
| 1 | 8 | 11.11 |
| 0 | 9 | 0 |
| 7 | 2 | 77.78 |
| 8 | 1 | 88.89 |
| 9 | 0 | 100 |
Calculate winning percentage by giving a try to the win percentage calculator.
Working of the Winning Percentage Calculator:
The simple processing of the win loss percentage calculator is elaborated below:
Input:
- Add the number of Wins
- Add the number of losses, ties.
- I want to give ties any value, then add that specific values
- Press the Calculate button
Output:
The free wr calculator does the following calculations:
The winning percentage is displayed.
Press recalculate button if want to find another value
FAQs:
How do you calculate winning percentage with ties?You are easily able to add the wins and losses easily, but when adding ties add certain values like ½ for loss or ½ win add the values in the win ratio calculator and specify the value of ties.
What is a win to loss ratio?It is the measure of the ratios of a person or team’s success in a particular competition.
Why do we need a winning percentage?
Winning percentage makes us sure about the rate of winning of a particular team and its average rate of winning.
How to find win percentage?
If you want to calculate the winning percentage, divide the total number of games played against the number of losses and wins together.
Calculate winning percentage by using the win loss percentage calculator.
How is win probability calculated by using a win loss percentage calculator?
For example, if a team has a winning ratio of around 80%, it means this team has a probability of winning 8 games out of 10.
Conclusion:
The winning percentage calculator has broad importance in the field of sports. It is vital to understand the capability of individual player performance and team performance. This can be great to analyze the whole competition and winning probabilities of different teams.
References:
From the source of Wikipedia: Winning percentage, Discussion, Statistics, Major League Baseball.
From the source Americanfootballdatabase: Winning percentage, Statistics, National Hockey League
From the source excel.tips.net: Counting Wins and Losses, More ExcelTips
The NBA 90,000 is a fashionable numbers empire. Explaining how to use advanced statistics - openers - Blogs
Historically, statistics in sports has been taken as such a factual argument.
In endless disputes and ratings saturated with subjective perception, it is cold numbers that are an indestructible foundation that is definitely not biased. The statistics take into account every possession of every match. Statistics don't hurt anyone.
The numbers certainly give accurate answers. Just not all questions. You need to put them in the right context in order to come to adequate conclusions. You need to understand what statistics take into account, and what can be missed.
One of the main components of working with statistics is, in fact, the choice of the considered metrics. Statistics are evolving and new indicators are emerging. And the game is changing, and some data is no longer as useful as it used to be.
So what statistics are relevant today? What metrics have already become obsolete? Which of the new indicators is the most useful? Let's figure it out.
Team statistics
It is more logical to start with a few banal, but important and fundamental things.
Such as attacking or defensive rating and 4 factors.
Points per 100 possessions
Back in the day, teams' defense and attack were measured by points conceded or scored per match. Today, everything is a little more accurate. Instead of "per match", "per 100 possessions" is used, which is called the attacking and defensive rating . This allows you to make an allowance for the pace and not talk about the fact that any fast team cannot defend, but attack smartly.
Here's a simple example: The Bucks are now by far the best defense in the NBA, only conceding 101.6 points per 100 possessions. But in terms of points missed per game, Milwaukee is only fifth in the NBA. Why? Because they play fast enough, and the opponent simply has more attacks per match (as well as the "deer" themselves). But on any given defense, the Bucks have fewer passes than any other NBA team, so a defensive rating is clearly a more useful tool here.
Same with attacking rating, as an alternative to match points.
These two indicators most simply and accurately describe the level of the team on both sides.
The difference between a team's attacking and defensive rating is called "no-rating", in fact, it is the difference in score or +/-, but in terms of 100 possessions. This metric is quite indicative and allows you to assess the strength of the team almost better than the win-loss ratio of .
The idea is something like this: if you have a lot of wins, but not the highest net rating, then most likely you suffered several big defeats, could not confidently beat weak teams and took some tight matches with a close ending, which always implies a factor chance. Naturally, this should impose a certain filter on the perception of the percentage of matches won.
Of course, Denver will tell everyone that he just plays well in the decisive minutes and rightfully wins ahead of Utah, Dallas and Houston, even though they have a higher net-rating. Only for some reason, Utah has a higher percentage of wins in games whose outcome is decided in the last minutes.
We can say that this indicator underestimates the importance of hard-fought endings and overestimates the importance of crushing matches. And we can say that it allows you to make an allowance for luck. Not always and not for everyone, “no rating” will be more objective than a simple number of wins, but when comparing teams with a similar number of wins and losses, a noticeable difference in “no rating” is definitely important.
4 factors
Attack and defense ratings are such generalized indicators that show the overall strength of the team in each half of the court. For more detail, indicators of the so-called 4 factors are very useful.
So-called, because, in fact, there are 8 of them: four in attack and four in defense. This includes effective hitting percentage, rebounding percentage, turnover percentage, and free throw frequency. Together, these indicators give a fairly complete picture of the team's game.
Effective field percentage (eFG%) measures the accuracy of shots.
Previously, the base percentage from the field (FG%) was used - the number of hits from the number of shots. But with the growth in the number of three-pointers, this metric is hopelessly outdated. She mixes shots from behind the arc and two-pointers, which seriously hits teams that rely on three-pointers. The bottom line is that “three-pointers” are not sold so often, but they cost one and a half times more, and FG% only takes into account accuracy. eFG%, in turn, also adjusts for the value of three-pointers . In fact, an eFG% of 50 means the team scores 1 point per shot.
So, Houston is 22nd in field shooting and 6th in eFG% because almost half of their shots are 3-point shots. And, given that they have the second offense in the NBA, the advanced figure is clearly closer to the truth. eFG% allows you to noticeably more adequately assess the effectiveness of the throws of the team and the opponent.
The percentage of losses and the percentage of rebounds shows who actually had more of these shots.
If you rarely lose the ball and often rebound on offense, then you are more likely to hit the ring. This can help out even with not the highest throw efficiency. Again, it is in percentage terms that such data is more useful. They allow you to count not the number of losses per match, but the number of losses per 100 possessions. Not the number of rebounds in the game, but the percentage of available rebounds. This makes more sense.
For example, Utah and Miami are near the middle of the table in losses per match. But their percentage of losses is at the level of 6-7 places in the League from the end. That's because they play very slowly and they just have fewer possessions per game, which means they're less likely to lose the ball. But in each individual attack, the chances of making a loss are quite high.
The last component of the 4 factors is the FTA rate. This is the number of shots from the line for 1 shot from the field. And this indicator kind of closes the topic.
Because if the team didn't lose the ball, it doesn't mean that it definitely threw a field goal, it may have earned free kicks. This must be taken into account. But theoretically, one could remove this factor from the list by replacing eFG% with TS%. True shooting is another combined accuracy metric that takes into account the value of shots, and it includes not only two-pointers and three-pointers, but also free throws . Then the throws from the line will be taken into account. But, of course, the frequency of free throws gives a more complete picture of the game.
In general, 4 factors describe the match quite fully. As a rule, looking at them, you can determine who won, although there is no mention of points in these statistics. And, if you look at the seasonal performance of the team in 4 factors, you can quickly find out what exactly the indicators of the attacking and defensive ratings are made up of.
Distribution of throws
Now in Moscow living rooms there is only talk about the effectiveness of throws.
Many are already simply sick of this efficiency, because "how much can you throw your threes." As if if the player takes two steps forward and scores one point less, the game will immediately become still beautiful. As if, if the player opens on the middle, and not in the corner, it will become easier for his partners to go into the passages everyone loves.
In fact, the idea of efficiency is much broader. It was never "throw only three-pointers." It was always "throw lay-ups, three-pointers (preferably from the corner) and try to get free throws." And it's just a matter of mathematics. Because some attempts are more useful than others. On average, a 3-pointer from the corner earns more points per shot than a 3-pointer under 45. A lay-up promises more points per shot than a floater. A three-pointer in the forehead brings more points than a long-range average. A pair of free throws is worth more points than any field goal other than a dunk (but if you count all shots from under the basket, then their implementation is lower than free throws).
That's why the teams are trying to get to the big points in the attack and defend themselves in such a way as not to give the opponent profitable shots. And this gives a new look at the throw card - makes it a kind of measure of success. Because the accents are now so pronounced that the ability to get the right throws is already a victory. A high number of attempts from good positions means that you are generating opportunities for correct shots, despite the fact that any opponent knows that these are the ones to try to avoid.
Of course, the set of players does not always allow you to get the most out of the situation. Chicago is the first in the NBA in shooting from under the basket, but the last in the accuracy of these attempts. “Golden State” rarely allows the opponent to throw from under the basket, but misses everything from there. Minnesota shoots a lot of three-pointers, but rarely hits them (perhaps why they are given these shots so easily). And last year's Spurs, on the contrary, constantly threw with an average, but they did it so accurately that a mathematically incorrect throw turned out to be quite effective (although it turned out to be impossible to throw with such a percentage two years in a row).
Performers are important. But they will not turn the math upside down, they can just correct it a little. The worst team in shooting from under the basket still shoots more than 62% from there, that is, 1.24 points per shot. The worst team at 3-pointers from the corner hit 33.9% of their attempts from there, which is more than 1.01 points per shot. No one in the NBA shoots above 48 percent (0.96 points per shot) from any medium range.
Any team will shoot more efficiently by coming up with the right shots. And by removing advantageous shots from your opponent, you improve your defense.
Therefore, the distribution of shots by distance and accuracy in each of the categories is one of the tools for evaluating a team in both halves. In principle, this can be used as a kind of “adjustment for luck”. If a team takes disadvantageous throws, then it should not have too high a conversion. If a team gives the opponent good shots, and he misses them, sooner or later it will end.
Quite conveniently, distance throws are presented here in the team shooting/opponent shooting section. There are share of shots, and implementation, and separate columns for three-pointers from the corner. The data can be rewound back to the year 2000 if it is interesting to see how teams threw before, and how they throw now.
Theoretically, from all this abundance of team indicators, one can even form a certain game pattern for oneself.
For example, a defensive rating would show that the Jazz and Bulls have about the same level of defense. Four factors will make it clear that "Utah" almost does not force losses, and "Chicago" - on the contrary, very much succeeded in this. The throw card will show that "Utah" does not let anyone near its ring - the opponents almost do not attack from close range, and against the "bulls" they only throw them on the way.
As a result, it is logical to assume that Gobert sits under the basket, does not meet the opponent's ball handler, and therefore does not force him to make mistakes.
From here, Utah's opponents have few losses. But with such a defense, Gobert can completely block the “paint”, which is what the throw card shows. With the "bulls" the opposite is true - high pressure on the ball forces the opponent's mistakes, but in case of failure, they open both a dash to the ring and three from the corner.
But this is theoretical, because I did everything the other way around, first I looked at the games, and only then - the statistics.
What to get stuck in quarantine
This is not exactly team statistics, but it is not individual either. In general, NBA.com now has two very interesting tools for assessing the success of certain combinations of players.
For example, the impact section allows you to understand how certain players affect each other and partners. For example, you can see how Harden and Westbrook interact. Are the Rockets' no-ranking better when they're both on the floor, or when Harden plays without Westbrook? Does Russ shoot more accurately when Harden is on the floor? Does the defense get better with both of them on the bench? Does Rivers shoot more accurately playing only Harden or only playing Westbrook? Everything has already been calculated.
This is quite an important thing when evaluating team leaders. Can they play without each other? Do they make each other better? And, as a result, is it worth it to breed them by the minute?
You can also look at the influence of players from different teams in matches with each other, but here, for obvious reasons, the sample does not allow drawing conclusions (at least in the regular season). If we look at the opposition of the players, then the statistics on match-ups are more indicative. The metric allows you to see both who usually defends against whom, and how successful different players are in such matchups. For example, who LeBron attacks through most often or against whom he throws the worst. The sample is again small, but describes the extreme cases accurately. If someone can't defend against LeBron it shows immediately, if someone does a really good job it shows.
The second interesting section is lineups. All the top five in the NBA on one page.
The visualization is very convenient, you can immediately see which combinations played a lot, and which ones were the most successful.
Combinations can be sorted not only by "no-rating", but also by accuracy, the efficiency of the opponent's shots and the share of shots scored in the early attack. Naturally, it is not necessary to be tied specifically to the fives - you can look at combinations of 2, 3 or 4 players.
Player statistics
Individual data is mainly compiled from three statistical sections. The first is the load, the amount of work in the attack. The second is the efficiency of this work. The third - at least something about protection.
Throws
Let's start with the engagement percentage (USG%). The metric takes into account productive attacking actions - shots, free throws and losses. USG% is the proportion of possessions in which the player made such an action during the time he was on the court (possessions spent on the bench are not counted as idle).
Basically, this reflects the shooting load, allowing you not to collect free kicks, field goals and losses separately in the corners. At the moment, the NBA leader in this indicator is Giannis, he has an engagement percentage of more than 37. That is, when he is on the floor, 37% of the Bucks' possessions end with an attack by the Greek. Which is not surprising, given his 20 field goals and 10 free throws in 30 minutes on the floor. This is the seventh most in history, above only Bryant, Jordan, Harden, Iverson and Westbrook (twice). At the same time, in terms of efficiency, only Harden is next to Giannis, the rest are noticeably lower.
As for efficiency in general, it is quite well described by the same eFG% or TS%. They make allowance for the value of the rolls and bring all the indicators together. But there are important details to consider.
Was the throw after the pass or not?
Other things being equal, it is easier to get from the transfer.
It would seem that these are the problems of those who throw from the dribble, but these players are more independent, because they themselves bring themselves to the throw. They are more difficult to neutralize. But among the attacking players after the transfer, there is a certain line between really dependent players and just players of this specific type. For example, Redick shoots after a pass, but sort of goes to the throw himself. It opens so that any log can give it a pass. He doesn't need a point guard, just an average NBA player. On the other hand, it takes a certain amount of talent to flirt with some pick-and-roll centers - the point guard must pull two on the screen in order to free his big one. For different types of players, the degree of dependence is different, as is the adjustment for the fact that they attack after the transfer. Therefore, the next question is:
In which attack were points scored?
NBA.com now has a division into types of combinations.
By opening a specific sub-type of attack, you can see how often the player uses it and how many points he scores for such possession.
So, different types of holdings have different efficiency. If the performer is qualified, then throws from under the basket after a partner's discount are worth more than 1.3 points per possession. Throws from top rollmen are worth more than 1.2 points per attempt. Approximately the same amount is given by "spot-up attempts" - throws after discounts, when the shooter did not open on the screen to receive, but simply remained open due to the fact that the opponent went somewhere to help. This is dependent throws. They are easy to hit because your partner creates them for you.
Of course, it should be noted that, for example, a competent type rollman attracts so much attention to himself that it facilitates the work of the ball handler and gives almost an inverse relationship. But these are particulars from the red book, they are rare in the wild, and even successful rollmen are, for the most part, dependent and easily replaced players.
But screen openings, pick-and-rolls, isolations and post-ups are possessions created by the thrower himself. They require more aggressive movements, it is already more difficult to maintain balance and withstand the mechanics of the throw, it is more difficult to hit. Hence the drawdown in terms of efficiency in the region of 1.1 points per possession from the best representatives of each of the types.
Was the throw in position or early attack?
Milwaukee is the most effective field goal shooter this season with an eFG% of 55.3. The worst team in terms of accuracy on early offense is the Clippers, who hit with an eFG% of 56.0. That is, the worst transition in the NBA is more productive than the best offense in the league. So, naturally, it is easier for players to hit in early attacks, and those who have a high share of shots in transition are initially in a winning position. And it's one thing if you're Giannis or Simmons, the player who actually creates these early offensive opportunities.
It's another matter if you're just defending at the top and when intercepted, you find yourself closest to someone else's ring. You are a good fellow for running fast, but that's all.
And the effectiveness of the players must be run through such filters. Because the most accurate basketball players will always be centers who shoot 3 times per game, and all three of their shots are dunks after the transfer of a partner. But this does not mean that they are the most effective scorers. They just have the easiest job.
Passes
The second component of the attacking load is passes. It seems logical to use the percentage of assists (AST%) . The indicator takes into account the share of partners' hits from the player's pass from the total number of partners' hits. That is, if Valera has AST% 20, and the guys who play with him on the team hit 10 times, then Valera has 2 assists. But the trick is that possessions in which the player threw himself do not count at all.
Therefore, AST% is slightly higher for stars with a large throwing load, the lion's share of those shots for which they did not give a transmission are their own.
On the one hand, the assist percentage approach is logical. Because players with a high shooting load simply have fewer opportunities to give an assist - there are fewer possessions in which they pass. And it seems to be more correct to count exactly how many assists from the theoretically available ones the player has given, and he cannot give an assist to himself.
On the other hand, if you are constantly throwing, then the possessions that your partners hit are stupidly smaller, and it is easier to have a high share of passes there. So part of the lack of focus on the pass will make your percentage of assists higher, which does not sound very logical. In general, the metric is ambiguous and favors players who dominate the ball.
If you need to calculate a purely passing load, then it is more appropriate to take "effective passes per 100 possessions.
" In essence, this is the percentage of team attacks that ended with a pass from a player. Adding this to the percentage of engagement, you can roughly estimate the total load in the attack. Then a large throwing load will be taken into account, and players who throw rarely will not be pinched.
But the engagement percentage takes into account not only hits, but also all throws, and even losses. To add to it exclusively assists is not logical.
Potential assists will come to the rescue - passes that did not lead to a hit, but to a throw (naturally, including hits) .
This is especially handy if you're Trae Young, playing with hand-assers who can't hit anything. In assists per 100 possessions, you will be inferior to Doncic or Rubio, but you will be higher in chances created. And this is important, because point guards, who play with weak finishers, are initially in losing positions, and then they are pulled up.
On the other hand, this metric plays into the hands of guys who are just so bad at passing that it's impossible to shoot properly from their pass.
Westbrook has more potential assists than Harden, and James has more actual assists. And any Oklahoma fan who has seen how a real point guard should play this season knows what it is.
In any case, in order to somehow use this metric, you need to wait for NBA.com to allow you to see data in terms of 100 possessions, and not “per game”.
As for the effectiveness of transmissions, it is considered by different methods, but not all.
Ancient as the world option - the ratio of transfers to losses . But, like everything ancient, this metric is rather raw. Such statistics will always favor players who aggravate little for themselves and are aimed precisely at the draw. Because surprise is surprise, the ball can be lost not only when trying to pass. Rubio has a better pass-to-loss ratio than LeBron, not because he's a better passer, but because LeBron does a lot of other things besides passing, and that's where you can lose the ball.
Today there are still not too perfect, but already more interesting methods.
For example, thanks to tracking, you can find out what percentage of a player's passes were successful (AST to PASS%). Here, of course, you need to compare only those who at least sometimes pass. But, in general, the tool is working and shows how aggressively the player sharpens.
More complete data available (AST to PASS% adjusted) . This takes into account the percentage of passes that led not only to a hit, but also to free throws or an assist (that is, hockey assists are counted). When it comes to players with a high overall playload, this is probably the most logical tool for evaluating passing performance. No, not because Booker and Young are higher than LeBron in this indicator. It's just that this metric shows what part of the programs are really aggravating.
But that number doesn't really honor 3-point passes. The chance that a discount on a long shot will be effective is initially lower, simply because of the conversion percentage, so the percentage of passes that turn into assists will be lower.
But a three-pointer is more expensive. From this point of view, it is more logical to use the points scored after the player's passes. But this, in turn, has nothing to do with efficiency, because it does not take into account the proportion of successful transfers from the total amount given. This is not to mention the fact that on the official website of the NBA, again, this data is available only in the “per match” format, which is unfortunate. For, as already mentioned, such indicators do not allow accurate comparison of basketball players who receive different playing time and play at different paces.
In general, the transmission data has become more interesting, but there are still no clear answers.
Barriers
Well, for the "big" ones, involvement in the attack is decently reflected by screen assists. The screens that lead directly to a scoring shot show how often attacks actually go through those screens. Rudy Gobert is a recognized champion in this regard, he puts on 7 screen assists per match.
True, there are questions related to how much it is in the player setting the screens.
First, Adams is doing 5 screen assists per match this season, down from 3.4 the year before. You think it's Westbrook? If you rewind even further, there will again be 5 screens resulting in an average per game. And a year before that - again about 3.5. This indicator strongly depends on the game of the team. If they do pick-and-rolls that lead directly to the shot, then you will have a lot of effective screens. If not, then alas. Gobert tops screen assists not because he's a great screener, but because Utah plays through his screen every attack. How could it be otherwise, because if Rudy does not put up a barrier, then in attack it is just a useless piece of wood under the ring.
Secondly, the ability to make a screen is highly dependent on the player using the screen. For example, whoever Lillard is currently playing with, that “big” screen assist stat will be fine. Not only because Dame hits his pick-and-rolls over and over again, but because he does it so damn well.
In general, as an indicator of the quality of the screens, this metric is not very good. But as an indicator of the integration of the "big" into the attack - quite .
Protection
For a long time there were no sensible defensive statistics , and nothing has changed since then . Fans had to get by with blocked shots and interceptions, which were more bright manifestations than a reflection of real contribution.
But over time it got a little better, additional indicators appeared that are already more useful. And all the equally meaningless data appeared.
For example, attempts to rethink block shots and interceptions with a fashionable percentage of blocks or counting deflections (ball touches in defense) were initially doomed . Because they think the same thing just a little differently. And the problem with block shots and interceptions was not in the scoring model, but in their nature. These are rare tangible manifestations of defense, but they are not the goal, the mission of defense is to force a bad roll.
A block shot or an interception is more of a random consequence of a good defense. Well, Minnesota is in the top 10 this season in both steals and blocks per 100 possessions. I think it's not worth reminding where their protection is.
At the same time, it should be noted that good defensive players often ended up in the top in steals or deflections. It's just that there were also weak defensive players who took risks in an attempt to catch the interception. And their failures were not taken into account by statistics, but their successes were very much so. It's the same with players who cheat block shots by getting knocked out on every swing.
But with the development of tracking, it became possible to track the "protective percentage of the game" . And it became a real revolution, because now it was possible to clearly track which player through a certain distance hit the worst. What's more, this percentage was compared to the attacking player's average hitting percentage, so you can see how much the defender reduces the opponent's effectiveness.
So, the protective percentage under the ring showed who was the best rim protector. Today - Brook Lopez (5+ shots, 30+ matches).
And everyone was so happy, but this theme only really works for centers .
Because the centers protect the hoop from everyone. The center is almost impossible to hide in defense. And the perimeter players defend in their position. Therefore, they try to hide weak defensive players on someone harmless, and this allows these weakest defensive players to have a good defensive percentage. It's like telling what a historically tough guard Harden is in the post, like he's defending there against Embiid or other really post-up "big guys" that aren't that many in the NBA today. No, it's just that Harden is exchanged for the “fourth”, and then this “fourth”, who has not played with his back for two years, decides that it is his duty to trample Harden. James really does this.
By the way, you could look at the defensive types of possessions and evaluate the number of points a player misses in a given possession.
But pick and roll defense is the work of at least two people. Only protection against isolations and post-ups can really be assessed. And not only is this far from the entire defense, but there is not a single player in the league who has played at least 30 matches and defends in aizo or post-up at least 2 times per match.
In general, it is statistically difficult to assess the individual level of protection, even if we are talking about a banal one-on-one game.
Another sort of defensive indicator is defensive rebounding. And I just can't understand why anyone else cares about this indicator . Well, yes, if the ball is tossed, it will fall, and you caught it, great job. What is the value of the fact that it was you who caught the ball, and not your teammate? How many of your rebounds were actually snatched from the opponent and had any value? Today, defensive rebounds are like an attacking possession in which you didn’t allow a loss – that’s how it should be, there’s no need to count them.
Offensive rebounds look a little more interesting, but they tend to depend on the style of play and coaching attitudes. The pick-and-roll "big" chasing the ballhandler will often clean up after him. If the defensive center of the opponent is traded for the perimeter, then the attacking center has a height advantage in the fight for rebounding. And if you play for Popovich, then you can’t pick up rebounds in the attack - you need to immediately run to the defense. But there is at least something, focus on the rebound, instincts, hustle. There is nothing in defensive rebounding, as in individual metrics. Drummond collects 40 of them per match, no one cares.
But it got better over time. Accountants began to record not only the rebounds themselves, but also box-outs, now you can find out how many of the player's rebounds were torn out in the fight. Or to see that Drummond, who collected 10 rebounds on defense only last season, had no effect on Detroit’s team defensive rebounding, and Vucevic this season with 8.
5 rebounds on his shield, but with elite boxing numbers. strikeouts and rebounds with resistance - turns the work of "Orlando" on the shield.
Of course, defensive rebounding remains a relatively team topic because it is influenced by a lot of things. For example, a player can simply immediately run to the attack, forcing the opponent not to rebound, but to return to defense. The fact that the little one did not exchange on the perimeter, but worked on his feet and allowed the center to return under the ring to fight for rebounds, also has some value. But now there are more factors to know the real impact of a player on rebounding. And, in fact, the number of rebounds themselves is not important here at all.
Finally, one could evaluate the player's defense by looking at the defensive rating, but this never works because it depends heavily on the combinations the player comes out with. The very idea of assessing the individual level is lost.
In general, only the “big” players with their “paint” defense and influence on rebounds have decent defensive statistics today.
Something to get stuck in quarantine
There has always been a burning desire in the NBA to create some one indicator that would unequivocally explain who is the best player in the world. Previously, these were PER and WinShares - indicators that significantly overestimated the centers. Although MVP is still usually won by the person with the highest PER, John Hollinger's player performance rating.
Then there were more advanced and just other things: BPM, VORP, RPV, RPM, PIE and I made up one of these abbreviations.
Every time it's something new, and every time there are players who can hack the formula, like the centers once hacked PER (seriously, Whiteside is the 10th NBA player by this metric, John Collins is 13th, Mitchell Robinson - 14th, Wood - 16th, Harrell, Valanchunas and Drummond - close the twenty). Each new indicator has its weak point, because of which the formula overestimates someone. And, if the glitches of this metric are shoved into the top of someone superfluous, then how can you be sure that it adequately placed the non-superfluous in order?
In general, finding the perfect formula is rather utopian.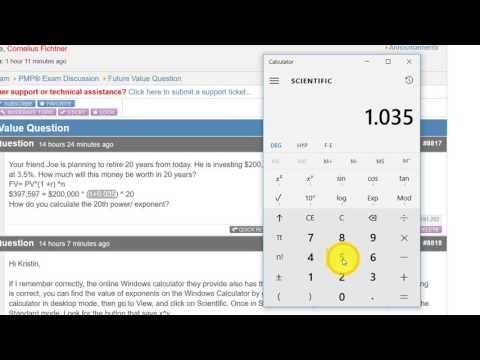
But it gives an alternative view, and allows something to be rethought a little. From the latest developments, the RAPTOP metric from 538 looks quite interesting.
In general, the development of statistics in recent years is encouraging. Now it is no longer a thin brochure, but a huge library in which you can dig for hours. The current statistics already have many more answers, and we are already accustomed to asking them many more questions.
But, of course, without context, these are still just numbers. Basketball VKontakte , Tom Pennington
Application of the Pythagorean formula | Applying the Pythagorean formula to football betting
The Pythagorean formula is primarily used for betting on American sports such as baseball and basketball, but can it be used for the same purpose in football? Analyst Mark Taylor explains why using this formula can be a potentially profitable strategy when placing bets in long-term betting markets.
One of the most famous mathematical and geometric theorems is the Pythagorean theorem, which establishes the relationship between the lengths of the three sides of a right triangle.
The Pythagorean formula explained After more than two thousand years, the famous baseball analyst Bill James reworked the equation of the theorem and used it as the basis for creating his own Pythagorean formula, which allows you to calculate the estimated winning percentage of the team in the context of gained or lost points or runs, not just based on the team's actual winning percentage. 9x).
Teams score goals more often than they win matches, and therefore this information gives a clearer picture of their true capabilities, since in a single match players score goals not only in situations where all the necessary conditions for this exist.
A team may score goals provided it is significantly ahead of its opponent, but it may also concede goals when the gap between the opponents is small. Data on in which situations and under what conditions teams score or, conversely, concede goals, obtained from the analysis of a small sample, can unnecessarily positively or negatively affect not only the team's winning percentage, but also the place it occupies in league ranking.
In short, a team that performs better than expected using the Pythagorean formula can be considered “lucky” and a team that performs worse than expected can be considered “unlucky”, but there is no guarantee that this state of affairs will be observed. and in the future.
This principle, first used only for baseball, then began to be applied to basketball and American football, and later to European football.
Application of the Pythagorean formula when placing bets on football Unlike predominantly American sports, in which matches rarely end in a draw, and therefore this factor is hardly taken into account, when using the Pythagorean formula to predict the results of football matches, players face a number of problems inherent in this sports discipline.
When using the Pythagorean formula, the biggest problems are the need to take into account the possibility of a draw, as well as environmental conditions that affect whether a goal is scored or not.
Given the fact that there are many different football leagues, in some of them the chances of teams to score a goal are higher than in others.
Also due to red cards, teams are sometimes forced to play with fewer than 11 players, which inevitably affects the number of goals scored.
Most of these topics are discussed in detail in this article by Howard Hamilton.
As in the original equation, James used the initial exponent equal to 2, but he changed the value of the exponent X, which reduced the standard deviation between the predicted and actual number of wins. In baseball, 1.83 is often used instead of a power of 2.
Football matches are predicted in a similar way, and the discrepancy between expected Pythagorean scores and actual scores in that sport is minimal if the exponent is 1.35 rather than 2.
Calculate winning percentage in sports in which a draw is rare or impossible, it is quite simple, but in football, a significant number of draws must also be taken into account for this.
Thus, the percentage of wins is often equated to the percentage of possible points scored, taking into account whether the team can score a point in a game with a draw, despite the fact that they did not manage to score a goal in this match.
In a season of 38 matches, a team receives three points for a win, for a total of 114 points. Based on this, a team whose goalscoring statistics indicate that their true winning percentage is 50%, according to this reasoning, can hope to finish the league season with 57 points.
Further modifications to the equation include changing the value of the components in the numerator and denominator, as well as the use of a raised number representing the number of goals scored and conceded to a power, which allows for variable conditions during the match that affect whether a goal is scored or not.
It is a common practice to use the Pythagorean formula to determine whether a football team's points in a season are justified in terms of goal statistics and whether these data can indicate that the team can continue to keep on this in the future.
level.
The probability of a draw for a team that rarely scores and concedes goals is higher than for a team that often scores and concedes goals.
The gradual decrease in the standard deviation (as the model improves) between the predicted and actual number of wins indicates how much it depends on the choice of exponent.
The value of the standard deviation using an exponent of two is 10 points for each team that participated in the 2014-2015 Premier League season. However, the deviation value is reduced to six points when using an exponent of 1.35, and if the exponent is calculated using environmental conditions on the field, then the deviation is reduced to a value of 4.4 points.
Determination of the total number of points scored in a season It is a common practice to use the Pythagorean formula to determine whether the number of points scored by a football team in a season is justified in terms of goals scored statistics, and whether these data can indicate that the team will be able to stay at this level in the future.
For the same purpose, and to distinguish between what is probably an essential element of luck and real skill, teams also determine the difference in goals scored.
Newcastle's 65 points in 2011/12 were almost 10 points above the standard Pythagorean expected for a team that scored 56 and conceded 51 goals.
Despite repeated victories thanks to just one goal scored and several serious defeats, the Newcastle team, which scored only five goals more than they conceded, is unlikely to be able to repeat a similar result again. Therefore, it is not surprising that in the 2012-2013 season the team scored fewer points.
The table below shows the number of Premier League seasons in which the currently top ranked teams performed above or below the expected Pythagorean score. For most teams, the performance in both cases is almost the same, which is quite expected, if we proceed from the fact that the luck factor is the main reason for their success or, conversely, failure.
| Team | Number of seasons with better than expected results | Number of seasons with less than expected results | Average points above and below expected results |
| Arsenal | 11 | 12 | 0.0 |
| Aston Villa | 10 | 13 | 0.3 |
| Crystal Palace | 3 | 3 | 0.0 |
| Chelsea | 13 | 10 | 0.4 |
| Everton | 7 | 16 | -0.6 |
| Leicester City | 4 | 5 | -1.8 |
| Liverpool | 5 | 18 | -1.7 |
| Manchester City | 8 | 10 | -1.1 |
| Manchester United | 17 | 6 | 3. 1 |
| Newcastle United | 11 | 10 | 0.8 |
| Norwich City | 5 | 2 | 3.3 |
| Southampton | 4 | 12 | -1.4 |
| Stoke City | 5 | 2 | 1.7 |
| Sunderland | 7 | 7 | -0.5 |
| Swansea City | 1 | 3 | -1.7 |
| Tottenham Hotspur | 14 | 9 | 1.2 |
| Watford | 0 | 2 | -2.4 |
| W.B.A | 3 | 6 | -0.6 |
| West Ham United | 12 | 7 | 1.1 |
Standing out from the crowd is Manchester United, whose total league points have surpassed goals scored and conceded in 17 of their 23 Premier League seasons.
This result was, of course, due to the fact that the team almost invariably played under the leadership of Sir Alex Ferguson, and additional research indicates that Manchester United players also have extraordinary abilities, thanks to which they manages to score winning goals in the last minutes of the match.
Eight of the ten teams that managed to exceed expectations and cause the greatest surprise in the history of the Premier League scored fewer points the next season, while nine of the ten teams that showed results that were below the expected figure calculated by the Pythagorean formula , in the following season were able to score more points.
Thus, there is a hypothetical suggestion that the apparent super-achievement of the Manchester United team under Ferguson (not taking into account current results) could be partly due to the level of preparation of the team members themselves.
On the other hand, Liverpool have performed worse than expected in 18 of 23 seasons, but there is little evidence that this trend is consistent.
In the eight seasons the team has played, its actual results have been three points or less than expected. On average, they were down 1.7 points during the season, nearly half of Manchester United's average points-over-performance.
Despite the attractiveness of descriptive data showing a team's consistent tendency to perform better or worse than expected Pythagorean results, in many cases a team's subsequent league performance is more in line with previous Pythagorean results. than the total actual number of previously scored points.
How to effectively apply the Pythagorean formula All-time Premier League data suggests that actual points scored in one season correlate better with last year's expected Pythagorean score than with actual points scored in the previous season.
The most notable case in this regard was in 1992-1993, when Norwich finished a 42-game Premier League season in third place with 72 points despite scoring 61 goals. times, and missed - 65. In 16 matches, the victory was achieved thanks to a difference in the score of one goal, however, the expected indicator calculated by the Pythagorean formula for the team was 55 points, and in 1993-1994 Norwich fell to 12th place with 53 points .
