Home »
Misc »
How to use math in basketball
How to use math in basketball
Math in Basketball – How Math Is Used in Sports – Cool Math
At first glance, basketball and math seemingly have little in common. While basketball is hugely popular in American schools, math has a considerably smaller fan following. However, a closer look at the sport reveals that there is a considerable amount of math in basketball. Pointing out how math is used in basketball is a great way to get your kids more excited about angles and percentages, while helping them realize how important math is in everyday life.
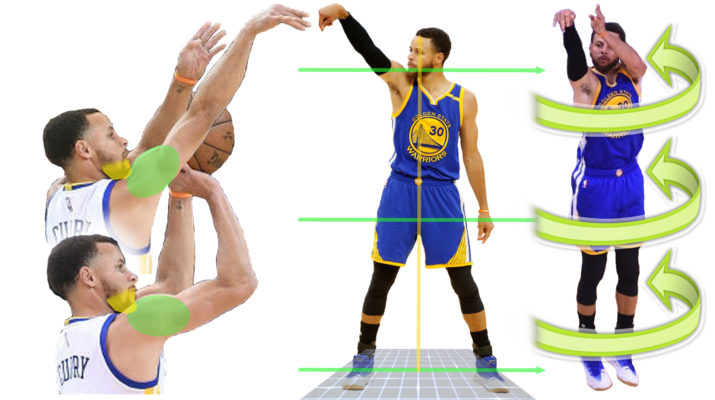
The angle at which the ball is thrown is determined as the angle made by the extension of the player's arms and a perpendicular line starting from the player's hips.The math in basketball involves a wide range of math topics. Kids can practice geometry, percentages and even basic mathematical operations while playing or watching a game of basketball.
Whether they realize it or not, basketball players make use of many geometric concepts while playing a game.![]() The most basic of these ideas is in the dimensions of the basketball court. The diameter of the hoop (18 in), the diameter of the ball (9.4 in), the width of the court (50 ft) and the length from the three point line to the hoop (19 ft) are all standard measures that must be adhered to in any basketball court. Knowing these measurements is useful for kids who would like to practice basketball at home without access to a full-fledged basketball court.
The most basic of these ideas is in the dimensions of the basketball court. The diameter of the hoop (18 in), the diameter of the ball (9.4 in), the width of the court (50 ft) and the length from the three point line to the hoop (19 ft) are all standard measures that must be adhered to in any basketball court. Knowing these measurements is useful for kids who would like to practice basketball at home without access to a full-fledged basketball court.
The path the basketball will take once it’s shot comes down to the angle at which it is shot, the force applied and the height of the player’s arms. When shooting from behind the free throw line, a smaller angle is necessary to get the ball through the hoop. However, when making a field throw, a larger angle is called for. When a defender is trying to block the shot, a higher shot is necessary. In this case, the elbows should be as close to the face as possible.
Understanding arcs will help determine how best to shoot the ball. Basketball players understand that throwing the ball right at the basket will not help it go into the hoop. On the other hand, shooting the ball in an arc will increase its chances of falling through the hoop. Getting the arc right is important to ensure that the ball does not fall in the wrong place.
Basketball players understand that throwing the ball right at the basket will not help it go into the hoop. On the other hand, shooting the ball in an arc will increase its chances of falling through the hoop. Getting the arc right is important to ensure that the ball does not fall in the wrong place.
The best height to dribble can also be determined mathematically. When standing in one place, dribble from a lower height to maintain better control of the ball. When running, dribbling from the height of your hips will allow you to move faster. To pass the ball while dribbling, use straighter angles to pass the ball along a greater distance.
Understanding geometry is also important for good defense. This will help predict the player’s moves, and also determine how to face the player. Facing the player directly will give the player greater space to move on either side. However, facing the player at an angle will curb his freedom. Mathematics can also be used to decide how to stand while going on defense. The more you bend your knees, the quicker you can move. Utilizing geometry, math in basketball plays a crucial role in the actual playing of the sport.
The more you bend your knees, the quicker you can move. Utilizing geometry, math in basketball plays a crucial role in the actual playing of the sport.
Statistics is essential for analyzing a game of basketball. For players, statistics can be used to determine individual strengths and weaknesses. For spectators, statistics is used to determine the value of players and analyze the performance of an individual or the entire team. Percentages are a common way of comparing players’ performances. It is used to get values like the rebound rate, which is the percentage of missed shots a player rebounds while on the court. Statistics is also used to rank a player based on the number of shots, steals and assists made during a game. Averages are used to get values like the points per game average, and ratios are used to get values like the turnover to assist ratio.
- Addition and Subtraction in Basketball
For young basketball fans, math in basketball is a great opportunity to practice simple skills like counting, addition and subtraction. Young kids can add up the points made in every shot to get the team’s total score. Kids can also be asked to use subtraction to determine how many points a team will need to catch up with the leading team, or to win the game.
Young kids can add up the points made in every shot to get the team’s total score. Kids can also be asked to use subtraction to determine how many points a team will need to catch up with the leading team, or to win the game.
Teachers: Math in Basketball ~ Activities | Get The Math
MEDIA RESOURCES FROM THE GET THE MATH WEBSITE
- The Setup (video) Optional
An introduction to Get the Math and the professionals and student teams featured in the program. - Math in Basketball: Introduction (video)
Elton Brand, basketball player and NBA star, describes how he got involved in sports, gives an introduction to the mathematics used in maximizing a free throw shot, and poses a related math challenge. - Math in Basketball: Take the challenge (web interactive)
In this interactive activity, users try to solve the challenge posed by Elton Brand in the introductory video segment.
- Math in Basketball: See how the teams solved the challenge (video)
The teams use algebra to solve the basketball challenge in two distinct ways. - Math in Basketball: Try other basketball challenges (web interactive)
This interactive provides users additional opportunities to use key variables and players’ individual statistics to solve related problems.
MATERIALS/RESOURCES
For the class:
- Computer, projection screen, and speakers (for class viewing of online/downloaded video segments)
- One copy of the “Math in Basketball: Take the challenge” answer key (DOC | PDF)
- One copy of the “Math in Basketball: Try other basketball challenges” answer key (DOC | PDF)
For each student:
- One copy of “Math in Basketball: Take the challenge” handout (DOC | PDF)
- One copy of the “Math in Basketball: Try other basketball challenges” handout (DOC | PDF)
- One graphing calculator (optional)
- Rulers, grid paper, chart paper, whiteboards/markers, overhead transparency grids, or other materials for students to display their math strategies used to solve the challenges in the Learning Activities
- Colored sticker dots and markers of two different colors (optional)
- Computers with internet access for Learning Activities 1 and 2 (optional)
(Note: These activities can either be conducted with handouts provided in the lesson and/or by using the web interactives on the Get the Math website. )
)
BEFORE THE LESSON
Prior to teaching this lesson, you will need to:
- Preview all of the video segments and web interactives used in this lesson.
- Download the video clips used in the lesson to your classroom computer(s) or prepare to watch them using your classroom’s internet connection.
- Bookmark all websites you plan to use in the lesson on each computer in your classroom. Using a social bookmarking tool (such as delicious, diigo, or portaportal) will allow you to organize all the links in a central location.
- Make one copy of the “Math in Basketball: Take the challenge” and “Math in Basketball: Try other basketball challenges” handouts for each student.
- Print out one copy of the “Math in Basketball: Take the challenge” and the “Math in Basketball: Try other basketball challenges” answer keys.
- Get rulers, graph paper, chart paper, grid whiteboards, overhead transparency grids, etc.
 for students to record their work during the learning activities.
for students to record their work during the learning activities. - Get colored stickers (optional) and colored markers, for students to mark the points and construct the trajectory, or path, of the basketball in Learning Activity 1 & 2.
THE LESSON
INTRODUCTORY ACTIVITY
- Begin with a brief discussion about sports. For instance, if any of your students play a sport, ask them to discuss the math they have used as athletes. Ask students what sports they like to watch and how they keep track of their team’s progress. Ask students to discuss the mathematics that players may use to track and maximize their performance.
- Explain that today’s lesson focuses on the use of math in basketball. Ask students to brainstorm how they think mathematics might be used in the sport. (Sample responses: knowing the rules of the game in terms of scoring, such as the shot clock timing, overtime, types and point values of shots and fouls allowed; knowing the dimensions of the court; statistical box scores, such as assists, turnovers, blocked shots, steals, field goal attempts, three-point goals and attempts, and playing time; ratios between two related statistical units, such as offensive rebounds and second-shot baskets, or two that contradict each other, such as assists and turnovers; per-minute and per-game statistics.
 )
) - Explain that today’s lesson features video segments and web interactives from Get the Math, a program that highlights how math is used in the real world. If this is your first time using the program with this class, you may choose to play the video segment The Setup, which introduces the professionals and student teams featured in Get the Math.
- Introduce the video segment Math in Basketball: Introduction by letting students know that you will now be showing them a segment from Get the Math, which features Elton Brand, an NBA basketball player. Ask students to watch for the math that he uses in his work and to write down their observations as they watch the video.
- Play Math in Basketball: Introduction. After showing the segment, ask students to discuss the different ways that Elton Brand uses math in his work. (Sample responses: He uses math to help improve his performance by using three key variables to influence his free throw shot; he uses acceleration of gravity or downward pull, the ball’s initial vertical velocity, and his release height to figure out the height of the basketball at any given time; he uses statistics to maximize the height of the basketball so it has the best chance of going into the basket.
 )
) - Ask students to describe the challenge that Elton Brand posed to the teens in the video segment. (The challenge is to use the three key variables and his stats to figure out the maximum height the ball reaches on its way into the basket in order to make a free throw shot.)
LEARNING ACTIVITY 1
- Explain that the students will now have an opportunity to solve the problem, which involves using the Fast Break Stats for information about the three key variables (acceleration of gravity, initial vertical velocity, release height) and Elton’s stats.
- Ask students to think of situations in their daily life where they may need to apply the concept of maximizing. (Sample response: finding the best price to charge for the school play to get the most people to attend while still making a profit.)
- Discuss why you would need to maximize the height of the basketball trajectory. (Sample responses: to make sure it reaches the hoop; the higher the shot, the further from the basket it peaks or reaches maximum height, increasing the likelihood the player will make the shot; higher arcs require a player to have more strength and use the proper mechanics.
 )
) - Review the following terminology with your students:
- Coordinates: an ordered pair of numbers that identify a point on a coordinate plane.
- Function: a relation in which every input (x-value) has a unique output (y-value).
- Acceleration of Gravity: causes a ball to speed up, or accelerate, when falling at a rate of -32 ft/sec2. Use only downward pull or half of -32 ft/sec2, which is -16 t2.
- Initial Vertical Velocity: the angle and speed when the ball leaves the player’s hand. Multiply by time to get the vertical distance traveled.
- Release Height: the starting position of the ball when it leaves the player’s hand.
- Trajectory: the path that a basketball follows through space as a function of time.
- Maximum Height: the value in the data set where the basketball reaches its greatest vertical distance at a given time on its way into the basket.
- Parabola: the graph of a function in the family of functions with parent function y = x2.
- The path of the ball when thrown is a trajectory represented by a parabola which can be modeled mathematically with a quadratic equation. This equation represents the position of the path over time.
- The height (h) of a ball, in feet, at a given time (t) is represented by the equation h(t) = -16t2 + v0t + h0 where v0 is the initial vertical velocity andh0 is the initial height.
- Vertex: the highest point of the parabola.
- Distribute the “Math in Basketball: Take the challenge” handout.
 Let your students know that it is now their turn to solve the challenge that Elton Brand posed to the teams in the video. Explain that in the activity, students should use the Fast Break Facts for information about the three key variables and Elton’s stats to figure out the maximum height the ball reaches on its way into the basket when making a free throw shot.
Let your students know that it is now their turn to solve the challenge that Elton Brand posed to the teams in the video. Explain that in the activity, students should use the Fast Break Facts for information about the three key variables and Elton’s stats to figure out the maximum height the ball reaches on its way into the basket when making a free throw shot. - Ask students to work in pairs or small groups to complete the “Math in Basketball: Take the challenge” handout. Use the “Math in Basketball: Take the challenge” answer key as a guide to help students as they complete the activity. Note: The handout can be used by itself or in conjunction with the “Math in Basketball: Take the challenge” activity on the website.
- If you have access to multiple computers, ask students to work in pairs to explore the interactive and complete the handout.
- If you only have one computer, have students work in pairs to complete the assignment using their handouts and grid or graph paper and then ask them to report their results to the group and input their solutions into the online interactive for all to see the results.

- Review the directions listed on the handout.
- As students complete the challenge, encourage them to use the following 6-step mathematical modeling cycle to solve the problem:
- Step 1: Understand the problem: Identify variables in the situation that represent essential features. (For example, use the three key variables: acceleration of gravity, Elton’s initial vertical velocity, and his release height.)
- Step 2: Formulate a model by creating and selecting multiple representations. (For example, students may use visual representations in sketching a graph, algebraic representations such as combining the three key variables and Elton’s stats: 24 ft/sec and a release height of 7 feet to write an equation that models the projectile motion, or an explanation/plan written in words.)
- Step 3: Compute by analyzing and performing operations on relationships to draw conclusions.
 (For example, operations include calculating the values of t when the ball reaches a height of 10 feet, the value of t when the ball reaches a maximum height, and the maximum height of the basketball at this time.)
(For example, operations include calculating the values of t when the ball reaches a height of 10 feet, the value of t when the ball reaches a maximum height, and the maximum height of the basketball at this time.) - Step 4: Interpret the results in terms of the original situation. (The results of the first three steps should be examined in the context of the challenge to maximize the height of the basketball during the free throw shot using Elton’s release height and initial vertical velocity, as well as the acceleration of gravity.
- Step 5: Ask students to validate their conclusions by comparing them with the situation, and then either improving the model or, if acceptable,
- Step 6: Report on the conclusions and the reasoning behind them. (This step allows students to explain their strategy and justify their choices in a specific context.
 )
)
Ongoing Assessment: Ask students to reflect upon the following:
- How can you combine the three key variables: acceleration of gravity, initial vertical velocity, and release height, to determine the maximum height of the basketball?
- At what time(s) does the ball reach 10 feet?
- At what time does the ball reach the maximum height?
- Is there only one path or trajectory for this to occur using Elton’s stats? How do you know? (You may wish to have students solve graphically to determine that this is the path using the given stats.)
- After students have completed the activity, ask students to share their solutions and problem-solving strategies with the class through discussion and visual materials, such as chart graph paper, grid whiteboards, overhead transparency grids, etc. Encourage students to discuss how their strategy helped (or didn’t help) figure out the maximum height of the path of the ball during the free throw shot.
 Ask students to discuss any difficulties they faced in completing the challenge and how they overcame those obstacles.
Ask students to discuss any difficulties they faced in completing the challenge and how they overcame those obstacles. - As students present their solutions, ask them to discuss the mathematics they used in solving the challenge. (Sample responses: Using a graphical model by plotting (time, distance) points for the start time and release height (0, 7), and the end time and rim height (t, 10) on a coordinate graph; representing functions using a mathematical model such as a table of values; identifying variables and writing expressions and/or a quadratic equation; using the properties of the graph of the equation to find the value of the x-coordinate of the vertex (), then solving the equation for t to find the maximum height at this time; using a quadratic equation and solving by factoring, completing the square, or the quadratic formula.)
- Introduce the Math in Basketball: See how the teams solved the challenge video segment by letting students know that they will now be seeing how the teams in the video solved the basketball challenge.
 Ask students to observe what strategies the teams used and whether they are similar to or different from the strategies presented by the class.
Ask students to observe what strategies the teams used and whether they are similar to or different from the strategies presented by the class. - Play Math in Basketball: See how the teams solved the challenge. After showing the video, ask students to discuss the strategies the teams used and to compare them to the strategies presented by the class. How are they similar? How are they different? During the discussion, point out that the two teams in the video solved the basketball challenge in two distinct ways. Discuss the strategies listed in the “Math in Basketball: Take the challenge” answer key, as desired.
LEARNING ACTIVITY 2:
- Go to the Math in Basketball: Try other challenges interactive. Explain to your students that they will use the web interactive to solve a series of problems similar to the one Elton Brand presented in the video segment. In this multi-level activity, students are challenged to use the 3 key variables, using a choice of player stats, to figure out the maximum height the ball reaches on its way into the basket to make the shot.
 Choices include: Initial Vertical Velocity of 5 feet, 6 feet, or 8 feet; Release Height of 20 ft/sec, 22 ft/sec, or 24 ft/sec. Students are encouraged to use the 3 key variables and the stats to calculate the ball’s height, h, at a given time, t, by setting up an equation to get started.
Choices include: Initial Vertical Velocity of 5 feet, 6 feet, or 8 feet; Release Height of 20 ft/sec, 22 ft/sec, or 24 ft/sec. Students are encouraged to use the 3 key variables and the stats to calculate the ball’s height, h, at a given time, t, by setting up an equation to get started.
[Note: As in Learning Activity 1, you can conduct this activity with one computer and an LCD projector in front of the entire class or your students can work in small groups on multiple computers. This can also be assigned to students to complete as an independent project or homework using the accompanying handout as a guide.] - Distribute the “Math in Basketball: Try other challenges” handout. Clarify and discuss the directions.
- Ask students to complete the handout as they explore the online challenges.
[Note: If you are using one computer, have your students work in pairs to plot points on graph or chart paper and to write the quadratic equation using the three key variables and the player’s stats. Have students take turns inputting their responses into the web interactive to test their choices as they determine the time(s) the ball reaches 10 feet, the time when the ball reaches maximum height, and the maximum height at this time.]
Have students take turns inputting their responses into the web interactive to test their choices as they determine the time(s) the ball reaches 10 feet, the time when the ball reaches maximum height, and the maximum height at this time.] - As in Learning Activity 1, encourage your students to use the 6-step mathematical modeling cycle as they develop a strategy to solve the challenges.
- After students have completed the activity, lead a group discussion and encourage students to share their strategies and solutions to the challenges. Ask students to discuss how they selected the equation and graphs used, and how they calculated the values for time and height using each set of player stats.
CULMINATING ACTIVITY
- Assess deeper understanding: Ask your students to reflect upon and write down their thoughts about the following:
- How did you determine an effective strategy for solving the challenges in this lesson? What are your conclusions and the reasoning behind them? (Sample answer: First you could find the total flight time of the ball.
 Since the height of the ball is a function of the time the basketball is in the air, and the path is a trajectory or parabola, it has an axis of symmetry that passes through the vertex or highest point. Students may use this fact to make a table of values, and since it is U-shaped between the two points it is at 10 feet, students may use the symmetry to include values to the left and right of the vertex. A trace function or key in a graphing calculator, as well as a sketch of the graph, may be used to solve the problem.)
Since the height of the ball is a function of the time the basketball is in the air, and the path is a trajectory or parabola, it has an axis of symmetry that passes through the vertex or highest point. Students may use this fact to make a table of values, and since it is U-shaped between the two points it is at 10 feet, students may use the symmetry to include values to the left and right of the vertex. A trace function or key in a graphing calculator, as well as a sketch of the graph, may be used to solve the problem.) - Compare and contrast the various algebraic and graphical representations possible for the problem. How does the approach used to solve the challenge affect the choice of representations? (Sample answers: If you decide to graph the points and then think of the basketball as an object that is traveling on a parabolic path, or trajectory, you would use this information to find the maximum height by finding the average between the two points it is at 10 feet; if you decide to write the equation of the function by combining the three key variables: acceleration of gravity, initial vertical velocity, and release height for Elton Brand or a given player, you could use transformations to write it in Standard Form for a quadratic equation, then find the times by using the quadratic formula or completing the square as algebraic strategies.
 )
) - Why is it useful to represent real-life situations algebraically? (Sample responses: Using symbols, graphs, and equations can help visualize solutions when there are situations that require using data sets or statistics to maximum performance of an athlete.)
- What are some ways to represent, describe, and analyze patterns that occur in our world? (Sample responses: patterns can be represented with graphs, expressions, and equations to show and understand optimization.)
- After students have written their reflections, lead a group discussion where students can discuss their responses. During the discussion, ask students to share their thoughts about how algebra can be applied to the world of sports. Ask students to brainstorm other real-world situations which involve the type of math and problem solving that they used in this lesson. (Sample responses: sports-related problems might include “catching air” in snowboarding, throwing a baseball or football, hitting a golf ball, and shooting a model rocket to maximize the height of the ball or rocket; maximizing the area of a garden/farm given specific fencing options; modeling relationships between revenue and cost.
 )
)
Research project of 7th grade students on the topic "Mathematics in Basketball"
Ministry general and vocational education
Sverdlovsk regions
Municipal autonomous educational institution -
secondary secondary school No. 91
in-depth study of individual subjects
MO City of Yekaterinburg
Chkalovsky district
Name sections (subsections): natural sciences (mathematics)
Research job: Mathematics in basketball
Author(s) of the job: Korshunov Maxim Alexandrovich , 7th grade
Khamidulin Andrey Sergeevich , 7th grade
Head (supervisors) of work: Grishina Anna Aleksandrovna ,
teacher Mathematics and Informatics
____________________
____________________
2020
Contents
Introduction. 3
3
Chapter 1 Mathematics and basketball. 5
1.1. Basketball game. 5
1.2. Game features. 6
Chapter 2.9
2.1. Location of players on the field. 9
2.2. Calculation of dependencies. 10
Conclusion. 15
List literature: 16
Application 1. The first rules of the game. 17
Application 2. Game basketball field. 19
Application 3. Questionnaire for 7th grade students. 20
Application 4. Survey results. 21
Application 5. Screenshot of the report of the results of checking the project file by the " Anti-plagiarism " system. 22
Mathematics is a science that studies numbers, quantitative relations and spatial forms. Mathematics is a subject that studies this science. We often hear and see such definitions. For us, mathematics is a way of describing various phenomena of nature and especially society. Since in Mathematics acts as an assistant in all spheres of human activity. For example, performing calculations when creating machines, exploring space, even creating literary works and that requires mathematics.
For example, performing calculations when creating machines, exploring space, even creating literary works and that requires mathematics.
We were interested in the question “Sport. Can mathematics to help this area of human activity with precise and strict language? Of course, the very first answer is chess.
But, we decided to check out other sports as well. Since we are already we have been playing basketball for several years, then our choice fell on this particular type sports.
The topic of our research is “Mathematics in Basketball”.
The purpose of the study : to study the impact of mathematics on basketball, to calculate the mathematical model of the best game with the maximum number of hits.
Tasks :
1. To study the literature on the research topic;
2. Compare and contrast common terms and concepts in mathematics and basketball;
3. Analyze the results obtained;
4. Show the application of the acquired knowledge in basketball;
Hypothesis: is it possible to build a mathematical model of an ideal basketball game.
Object research: mathematics and basketball.
Item research: mathematical component in basketball.
the following methods were selected : study of literary sources, processing of the received information, analysis, synthesis, research, practical.
Product project : creation of a mathematical model of the best game with the maximum the number of hits.
Practical significance : results can be use in additional education and self-education.
Basketball (basket - basket, boll - ball) is team game in which players throw the ball into the "basket", consisting of a ring with a mesh at the bottom. It is located at a height of just over 3 meters. from the floor (10 feet), to be more precise 3.05m. Picture 1
Dr. James is considered to be the founder of the game Naismith, who decided to diversify gymnastics lessons at the training center Christian Youth Association in Springfield, Massachusetts (USA) 1891.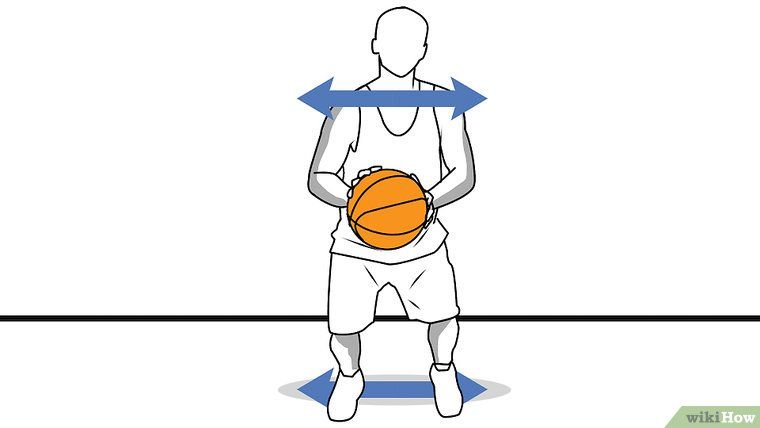 His idea was to throw a soccer ball in two fruit baskets without a bottom, which he attached to the balcony railing. Fans on the balconies they caught flying balls and tried to throw them into the opponent's basket, therefore, shields appeared that became the protection of the basket, and in 1893 appeared already iron rings with mesh. Given the shortcomings of the first matches, D. Naismith in during the year develops the first 13 points of the basketball rules (Appendix one).
His idea was to throw a soccer ball in two fruit baskets without a bottom, which he attached to the balcony railing. Fans on the balconies they caught flying balls and tried to throw them into the opponent's basket, therefore, shields appeared that became the protection of the basket, and in 1893 appeared already iron rings with mesh. Given the shortcomings of the first matches, D. Naismith in during the year develops the first 13 points of the basketball rules (Appendix one).
The new game was so addictive that in 1894 The first official rules were issued in the USA. Within 10 years basketball begins to "capture the world", first the East - Japan, China, the Philippines, and then the game comes to Europe, South America, the end of this journey becomes the Olympic Games in St. Louis (USA), where the Americans organized demonstration tournament between teams from several cities. Basketball was indicative also at the 1924, 1928 Olympics.
In 1923 France hosts the first international women's tournament, in which countries participated: England, Italy, USA. The game is gaining more and more popularity and recognition in the world, and at 1932g. was The International Basketball Federation (FIBA) was founded. The first composition of the federation included 8 countries - Argentina, Greece, Italy, Latvia, Portugal, Romania, Sweden, Czechoslovakia. In 1935, the International Olympic Committee decided to recognition of basketball as an Olympic sport. In 1936 at the Olympic Games in Berlin in the program appeared basketball. D. Naismith was the guest of honor of the games - creator of this game. Teams from 21 countries participated in the basketball tournament.
The game is gaining more and more popularity and recognition in the world, and at 1932g. was The International Basketball Federation (FIBA) was founded. The first composition of the federation included 8 countries - Argentina, Greece, Italy, Latvia, Portugal, Romania, Sweden, Czechoslovakia. In 1935, the International Olympic Committee decided to recognition of basketball as an Olympic sport. In 1936 at the Olympic Games in Berlin in the program appeared basketball. D. Naismith was the guest of honor of the games - creator of this game. Teams from 21 countries participated in the basketball tournament.
Basketball comes to Russia at 1906g, to the city - Petersburg, in the sports society "Mayak" and before the October Revolution 1917 remains the game only of this city. Actively play basketball throughout country begins after 1923, and the WTO began to participate in world championships from 1959
The game does not have one main technique, it includes various game techniques and performance variations.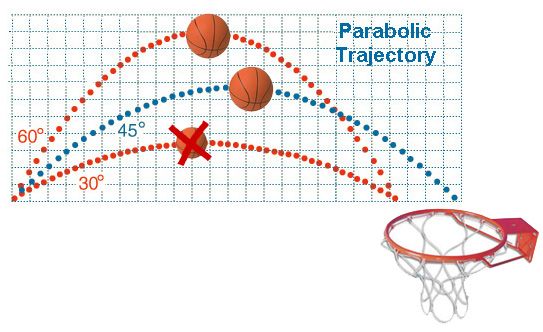 chief the rule for the player is: accessibility, rationality of actions together with purposefulness, jumps are accurate and fast, giving the player maneuverability on field.
chief the rule for the player is: accessibility, rationality of actions together with purposefulness, jumps are accurate and fast, giving the player maneuverability on field.
There are two teams of 12 people. There are 5 players from each team on the playing field. Goal: to score bigger opponent's ring the number of balls to prevent the second team from grabbing the ball and scoring into their own ring. Depending on the where the player throwing into the ring is located, a different number of points are counted for hitting. For a free throw 1 point is counted, for a throw from an average or close distance (in the jargon - paint) - 2, and 3 points given for a throw from behind the 3-point line. (Annex 2)
The ball is played with the hands only. Prohibited: running with the ball in your hands without hitting it on the floor, deliberately hitting it fist or leg, block with any part legs. Accidental touches with the foot or leg are not violations of the rules of the game. The beginning of the game is considered controversial throw in the central circle of the field, two players from rival teams.
The match is divided into four periods 10 minutes each (12 minutes in the NBA). Between the 2nd and 3rd quarters of the game is regulated break 15 minutes, other pauses are two minutes each, and in addition, coaches (in the NBA - and players) can take timeouts. After half the game, the teams must swap halves of the field.
The winner is the team that during the game was able to score more points. In case of a tie after the end of the regular time of the game, overtime is assigned, usually this is additional five minutes of play if given there is not enough time, the second, the third is assigned ... until one of the teams scores more points, and there is no the winning team is declared.
In order for the game to be effective and not like a chaotic movement around the field, roles assigned to players:
- point guard point guard or playmaker (eng. Play maker) - number one team responsible for choosing the combination of the game, which way to go and how build an attack.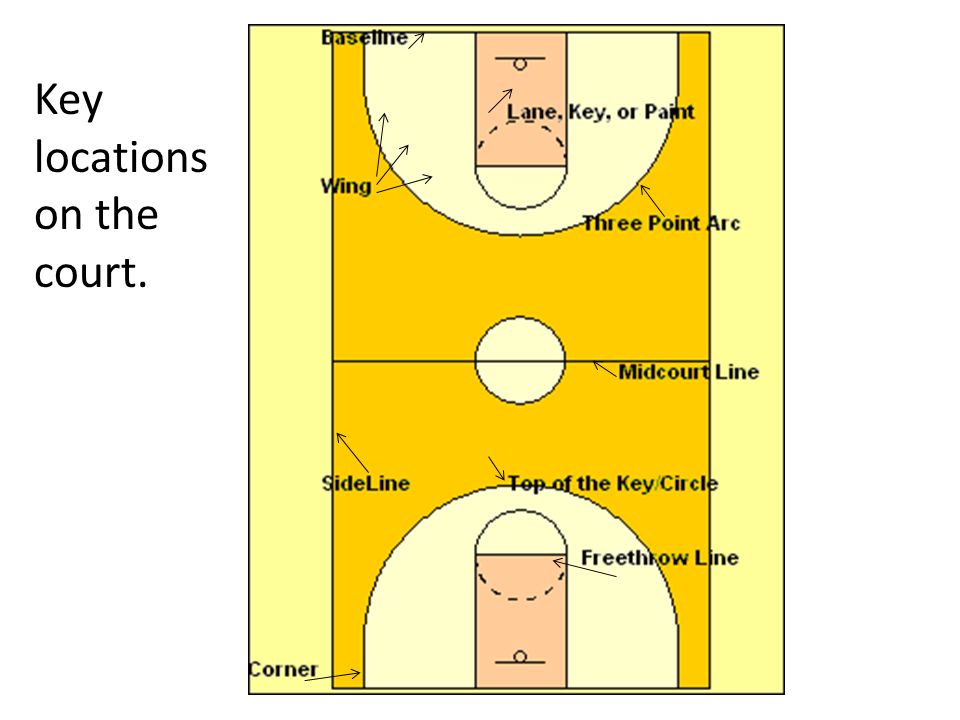 This player not only needs to see teammates, but also calculate the situation on the site.
This player not only needs to see teammates, but also calculate the situation on the site.
- attacks - perfect possession of the ball and movements;
- protection - possesses the skills of tackling the ball. The main goal of such a player is to insure team from a fast break of the opposing team.
Such division was in the past. In the modern professional basketball, priority is given to versatile players who combine the qualities which allow the player to play adjacent positions. This is how the position stands out comboguard (eng. Combo Guard). Based on the name, it can be determined that the player combines a combination of qualities necessary for defense and attack.
It is possible to classify players not only by type of activity on court, but also by height and weight:
- Average height 183-195 centimeters, weight 75-90 kilograms - this is point guard defender (eng. Point guard) or playmaker (eng. Play maker).
- Player average height 190-200 centimeters, weight 85-100 kilograms - attacking defender (eng. Shooting guard).
Shooting guard).
- Average height 195-210 centimeters, weight 95-110 kilograms - light forward (English Small Forward).
- The average height of a professional player is 200-215 centimeters, weight 105-115 kilograms - heavy forward (English Power Forward)
-Average height 210-220 centimeters, weight 110-125 kilograms - center (English Center).
Analyzing the game after training or a match often, you ask yourself: “Is it possible to improve your results or how to come up with the ideal model for the game and always score the maximum number of points?
To find answers to these questions, we decided to turn to our peers, but before that find out “How many of them know about this game generally?". For this purpose, a survey was conducted among 7th graders. (Annex 3)
As a result, we find that only 80% of the respondents know such a game, and about the rules and features in general, only 50%. Analyzing all this, we there was an idea to create a mathematical model of an ideal game, which means to solve the following tasks:
1. Reviewed various positions of the player on the field.
Reviewed various positions of the player on the field.
2. Formulas studied depending on the distance between the player and the basket.
3.According to with these formulas, the positions of the players of the school team were calculated.
4.Checked practical way these results.
Drawing 2
Depending on the position of the players located on the field in certain areas where they can best be implemented in accordance with their classification. Looking at the positions we investigated and got such a picture (Figure 2).
When a player "fouls" during a shot, then he gets on the penalty (in the figure - the yellow line) line and throws as many times he could score points on the throw - 1 point. Zone in which any goal will be counted as two points, shown in red in the figure. Purple zone - this is the zone in which any goal will be counted for 3 points. This is the location of the zones for the left ring.
Basketball - dynamics, movement speed and quickness. In addition, this competent execution of throws. At the same time, you need to know how to properly fulfill. Let's try to figure out how to throw the ball, under what angle and at what speed to hit the basket when throwing from different distances.
On average, a player makes about 20 shots from different distances and that the game is of high quality, and the player showed good results, he needs to distribute his forces throughout the game, without putting in too much effort. But the player not only throws the ball, but also overcomes the barrier in the form of a defender, for this the ball must be thrown through it and get into the basket. It is clear that the closer the defender is to me, then the higher the trajectory of the ball will be required, and then this is subject to constant hit. But people with 100% accuracy very rarely meet m, then additional calculations are needed.
Let's introduce some designations and consider their data:
1. D M is the diameter basketball ball. A standard basketball has a diameter of 24 cm.
D M is the diameter basketball ball. A standard basketball has a diameter of 24 cm.
2. m is the mass of the ball. In the standard is 600 g.
3.H - height hoops of a basketball hoop above floor level. In standard gyms - 3.05m.
4. D K - ring diameter, it is equal to 45 cm.
5. L - distance from the center of the ring to the place of the throw.
Figure 3
during the calculations, we will consider basketball ball with a material point, while neglecting the influence of air on the flight of the ball. Let's choose a system coordinates yOx to describe the movement: axis Ox - directed horizontally, the Oy axis is directed vertically, the origin of the coordinate system O coincides with the center of the ball at the start of the throw. Since the ball is moving with free acceleration fall g=9,8m/s 2 , directed vertically down, then using kinematic equations of motion we obtain:
, where v 0 x is the horizontal projection of initial ball velocity, v 0 y – vertical projection of initial velocity ball.
After mathematical transformations, we obtain the trajectory equation ball: , where α is the angle between the direction of the initial speed v 0 and the positive direction of the 0x axis, and the tangent of the angle α is:
, where β is the angle at which the ball flies into the basket.
After transformations of the equations, we obtain a formula for determining the initial velocity ball:
Performing calculations to find the initial speed at different throwing angles for different areas of the field (different types of points), we were several best angles are marked (Table 1). At the same time, in calculations, the growth the player was taken into account as the average height for our school basketball team 1.71 m. The flight path L changed depending on the location of the player along zones on the site, the angle α varied from 20 0 to 90 0 .
Table 1
| No. | υ 0 m/s | h, m | L, m | α |
| Single point zone |
| 1 | 5.61 | 1.71 | 4.3 | 30 0 |
| 2 | 4.8 | 1.71 | 4.3 | 45 0 |
| 3 | 4.1 | 1. 71 71 | 4.3 | 60 0 |
| Two-Point Direct Zone |
| 4 | 6.5 | 1.71 | 5.8 | 30 0 |
| 5 | 5.4 | 1.71 | 5.8 | 45 0 |
| 6 | 4.5 | 1.71 | 5.8 | 60 0 |
| Two-point side zone |
| 7 | 5.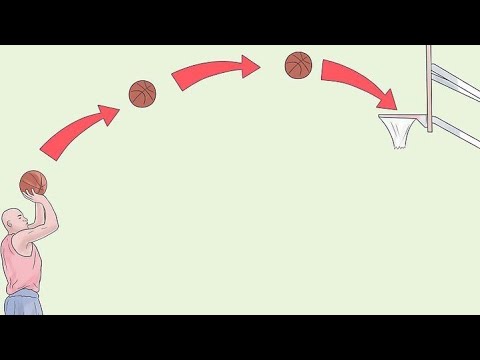 6 6 | 1.71 | 4.35 | 30 0 |
| 8 | 4.8 | 1.71 | 4.35 | 45 0 |
| 9 | 4.1 | 1.71 | 4.35 | 60 0 |
| Three-Point Direct Zone |
| 10 | 6.9 | 1.71 | 6.48 | 30 0 |
| 11 | 5. 7 7 | 1.71 | 6.48 | 45 0 |
| 12 | 4.7 | 1.71 | 6.48 | 60 0 |
| Three-point side zone |
| 13 | 7.5 | 1.71 | 7.55 | 30 0 |
| 14 | 6.1 | 1.71 | 7.55 | 45 0 |
| 15 | 5 | 1. 71 71 | 7.55 | 60 0 |
The selection of these corners is also related to the coverage area of the ring:
1. If the ball is thrown at an angle of 60° to the plane of the basket, then only 0.8661 parts of the ring are used.
2.If throw taken at a 45° angle, the target is 0.7071 rings.
3. When thrown under an angle of 30 °, the affected area is reduced to 0.5 rings.
Received the data helped us determine the ideal muzzle velocity for a given angle and flight path length.
Another factor affecting the flight of the ball is rotation ball. According to the rules, the ball must be thrown with reverse rotation. This is necessary in order to to keep the ball in its flight path, increasing the chances of hitting basket, by slowing down the speed of the ball. But it's all physical phenomena that we will not count.
As a result of calculations conclusions can be drawn:
- the smaller the angle throw, the smaller the chances of getting the ball into the basket, which means there should be increased accuracy. This can be achieved by increasing the height of the flight path.
This can be achieved by increasing the height of the flight path.
- the higher flight path, the longer the flight path of the ball.
- first case ideal and almost never found in sports, but the most acceptable throw angle ball 60 0 .
- attached at throw force determines the initial speed of the ball, which in turn determines the height of the ball's flight path. If you apply maximum force, then the accuracy will drop.
After analyzing all the results, we decided to check them on practice. Throwing the ball was carried out in accordance with the length of the trajectory flight and angle of inclination, which we first measured with a protractor. (Picture 4) In each of the cases, the hit was accurate, which means our calculations are confirmed.
Figure 4
6 30
0 ) (angle 60
0 )
affecting the quality of the throw, for example, physical and psychological.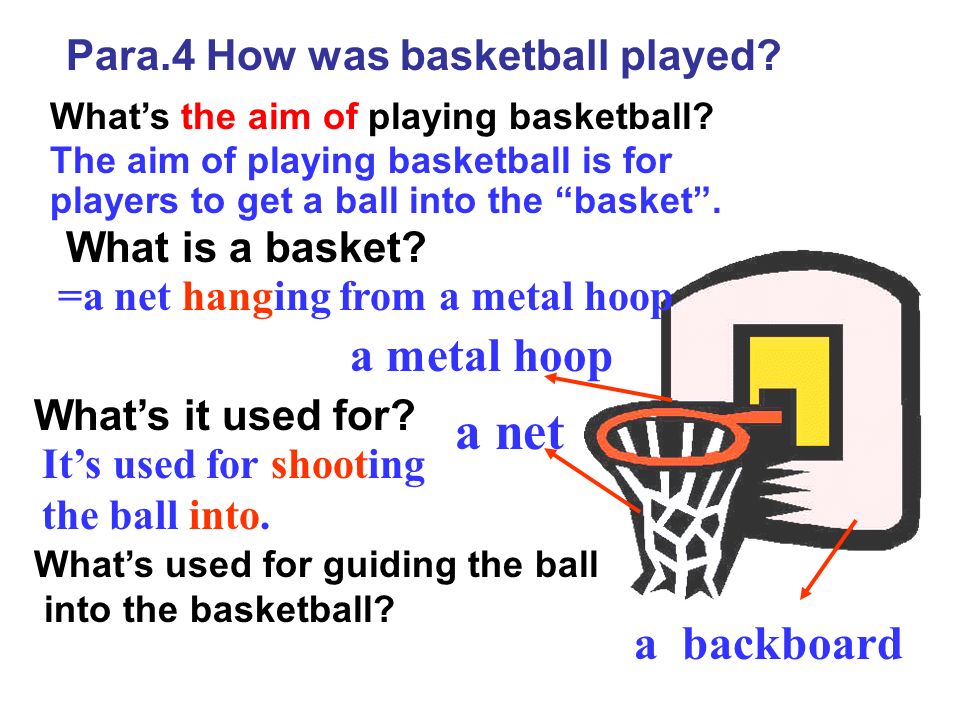 As well as in our calculations, we did not take into account physical phenomena and their calculations, which will be studied by us in the future in the course "Physics" and then our formulas and calculations will be finalized.
As well as in our calculations, we did not take into account physical phenomena and their calculations, which will be studied by us in the future in the course "Physics" and then our formulas and calculations will be finalized.
Working on this topic, we confirmed our hypothesis: it is possible whether to build a mathematical model of an ideal basketball game. But would like add that this is possible when taking into account a large number of factors - rotation ball, flight path, player height, etc.
In conclusion, we add that basketball is not only a beautiful sight sports, but the connection of physics and mathematics, where mathematics is an assistant.
For us, this project was the starting point in the study of only mathematics, physics, but in the awareness of the vast field of application of mathematics to human activity, and as Alfred said North Whitehead: "The most interesting property arithmetic is that it applies to everything: to taste sensations and sounds, to apples and angels, to thoughts and bones.![]() ”
”
1. Gershenzon EAT. Mechanics: Proc. Allowance for students. Higher pedagogical educational institutions / E.M. Gershenzon, N.N. Malov, A.N. Mansurov. - M .: Publishing Center "Academy", 200. - 384 p.
2. Pichurin L. F. Za pages of the textbook of algebra: book. for students in grades 7–9 avg. school - M .: Enlightenment, 1990.– 224 p.: ill.
3.http://sdushortambov.ru/index.php?option=com_content&task=view&id=73&Itemid=1
4.https://vm.ru/sport/163491-13-pravil-basketbola-dzhejmsa-nejsmita
5.https://sportyfi.ru/basketbol/priemi/peremeshchenie/
-o-pravilah.html
7.http://life.mosmetod.ru/index.php/item/kak-zabrosit-myach-v-basketbolnuyu-korzinu
8.http://images.yandex.ru
9.https://www.nkj.ru/archive/articles/33854/
1. The ball can be thrown in any direction with one hand (now you can throw with two hands).
2. You can hit the ball hit with one or two hands in any direction, but never with a fist (this hasn't changed, but accidental touches don't count).![]()
3. The player cannot run with the ball. The player must throw the ball from the point at which he caught it, an exception is made for a player running at high speed (now with the ball you can run).
4. Ball needed keep brushes. You can not use the forearms and body to hold the ball.
5. In any case hitting, grabbing, holding and pushing the opponent are not allowed. First violation of this rule by any player shall be called a foul; second foul disqualifies him until the next ball has been potted, and if any the obvious intention to injure the player is a disqualification for the entire game. At it is not allowed to replace a disqualified player. (now allowed 5 fouls with removal to the bench and replacement of the player).
6. Hitting the ball fist - violation of paragraphs of rules 2 and 4, the punishment is described in paragraph 5.
7. If any of side commits three fouls in a row, then a goal is recorded for its opponent (this means that during this time the opponent must not commit a single foul).![]()
8. Goal counts if a ball thrown or bouncing off the floor enters the basket and stays there. Defending players are not allowed to touch the ball or basket in throw moment. If the ball touches the edge and the opponents move the basket, then a goal is counted (now the ball bouncing off the floor does not bring points to the team, but the ball can be helped in flight).
9. If the ball goes out of bounds, he must be thrown into the field by the first to touch his player. In the event of a dispute, the referee must throw the ball into the field. thrower the player is allowed to hold the ball for five seconds. If he keeps it longer, then the ball is given to the opponent (nowadays, if the team is delaying time, they are given foul).
10. The referee must monitor the actions of players and fouls, as well as notify the referee of three fouls committed in a row. He is vested with the power to disqualify players according to rule 5.
11. The referee must watch the ball and determine when the ball is in play (inbounds) and when going into touch (out of bounds), which side shall be in possession the ball, as well as perform any other action that is normally performed by the referee (Now the referee can help the side judge).![]()
12. The game consists of two halves of 15 minutes each with a break of 5 minutes between them (now four games of ten minutes each. First and last break - two minutes, between halves - 15 minutes).
13. Party, scoring more balls during this period of time is the winner.
project "Mathematics and Sport" - Mathematics, Activities
Project "Mathematics and Sports"
8 9000 9000 9000 9000
Mathematics
Author of the work:
Widloga Daryan
Project manager:
Fedorova Olga Yuryevna
Institution:
MBOU "Secondary School No. the author set a goal to find out the influence of mathematics on the effectiveness of the game of basketball. To do this, a school student systematized and generalized knowledge about the relationship between mathematics and sports.![]()
More about the work:
In the student's research work in mathematics "Mathematics and Sports" , the author showed the significance and relevance of the relationship between mathematics and sports using the example of indicators. The project considered the basic concepts of mathematics and conducted research on the application of mathematical operations in sports - on the example of the sports game basketball.
Educational research project in mathematics on the topic "Mathematics and Sports" will be of interest to students in grades 5 - 8 of the school, is the definition of this science and the study of its application in various fields. The paper presents practical calculations and explanations of how mathematical norms are used in such a sport as basketball and how codependent these two areas are.
Contents
Introduction
1.Basic concepts of mathematics and the study of mathematical operations in sports.![]()
2. Application of mathematics in the game of basketball.
Conclusion
References
Introduction
What do mathematicians do and why are they needed at all? It is generally accepted that mathematicians sit at a desk all day long, come up with four-story formulas and harass a ream of paper a day. Most people do not think that they see the results of the activities of mathematicians around them every day. Without mathematical calculations, neither architecture, nor engineering design, nor even drawing up the mode of operation of traffic lights on busy highways is possible.
Mathematics and sports seem to be far from each other. But this is only at first glance. Mathematical methods are increasingly being used in sports.
It is known that the methods of mathematical statistics determine the prospects of athletes, the most favorable conditions for training, their effectiveness, process the readings of sensors that control the loads of athletes.![]()
Information theory makes it possible to estimate the degree of workload of the visual apparatus when practicing various sports. Mathematics and physics help to find the most successful forms of rowing boats and oars. math operations sports springboard
At the same time, playing sports has a beneficial effect on the mental activity and psyche of a person, strengthens his will.
Relevance of the project: we propose to consider the relationship between two different sciences.
Goal of the project: to learn the influence of mathematics on basketball performance.
Hypothesis: Mathematics plays an important role in the life of society.
Job tasks:
systematize and generalize knowledge about the relationship between mathematics and sports;
show the significance and relevance of this relationship on the example of indicators
Basic concepts of mathematics and the study of mathematical operations in sports
reality.![]() In close connection with sports, music, literature and many sciences, the stock of quantitative relations and spatial forms studied by mathematics is constantly expanding and filled with ever richer content. There are two kinds of mathematics:
In close connection with sports, music, literature and many sciences, the stock of quantitative relations and spatial forms studied by mathematics is constantly expanding and filled with ever richer content. There are two kinds of mathematics:
Mathematics is a science, the subject of which is artificial structures created by mathematicians in the process of their free creativity.
Mathematics studies " real " mathematical structures that exist independently of the mathematicians who discovered them. This is the so-called applied mathematics. For example, mathematics in technology, mathematics in ecology, mathematics in architecture, and among them - mathematics in sports. But the results of applied mathematics sometimes give unexpected and most important consequences. It is known that the methods of mathematical statistics determine the prospects of athletes, the most favorable conditions for training, their effectiveness, process the readings of sensors that control the loads of athletes.![]()
Applied Mathematics is designed to create, study, develop and improve methods of applying mathematics to problems that arise outside of it. The most important requirement for a mathematical model is its adequacy to the real object under study, i.e. in the correct description of the object according to the relevant characteristics. So, for example, a mathematical model of the game of tennis is built, which is adequate to the game in terms of the main characteristic - by changing the score in a game (set).
However, this model does not take into account emotional, psychological factors and adaptation to the opponent's game. Then this model is refined and another characteristic is introduced - adaptation or learning during the game. Yet this model remains inadequate to the real process in other respects.
Consider several practical tasks and list typical tasks that can be considered within the framework of the project using the methods of operations research theory:
Systems for organizing championships, tournaments and cup meetings (chess, tennis, hockey, etc.![]() ), ensuring the achievement of certain goals. For example, for: identifying the first and second winners of the cup meeting (subject to certain conditions).
), ensuring the achievement of certain goals. For example, for: identifying the first and second winners of the cup meeting (subject to certain conditions).
Thus, mathematics, and in particular applied mathematics, explains many sequences and patterns in sports. With the help of mathematical models, practical problems in sports can be solved, helping athletes and coaches achieve the highest results.
Applying mathematics to the game of basketball
Basketball is a popular sports game. For its more than a century of history, he has won a huge number of admirers around the world. The high emotionality and staginess inherent in it, the variety of manifestations of physical qualities and motor skills, intellectual abilities and mental capabilities attract the ever-increasing interest of millions of fans in our country as well.
Basketball consists of natural movements (walking, running, jumping) and specific motor actions without the ball (stops, turns, side steps, feints, etc.![]() ), as well as with the ball - (catching, passing, dribbling, throws). Confrontation, the goals of which are to take the opponent's basket and protect one's own, causes the manifestation of all physical qualities vital for a person: speed, speed-strength and coordination abilities, flexibility and endurance. Almost all functional systems of his body are involved in the work, the main mechanisms of energy supply are switched on.
), as well as with the ball - (catching, passing, dribbling, throws). Confrontation, the goals of which are to take the opponent's basket and protect one's own, causes the manifestation of all physical qualities vital for a person: speed, speed-strength and coordination abilities, flexibility and endurance. Almost all functional systems of his body are involved in the work, the main mechanisms of energy supply are switched on.
Achieving a sports result requires from the players: purposefulness, perseverance, determination, courage, self-confidence, a sense of teamwork.
Basketball is perhaps the only popular sport whose date and place of origin is known for certain.
As a physical education teacher and college professor at Springfield, James Naismith was faced with the challenge of creating a game for the Massachusetts winter between baseball and football. Naismith believed that due to the weather of this time of year, the best solution would be to invent an indoor game.![]()
In practical play activities, you can use mathematics as follows:
Know the geometry of the court: you need to know all the dimensions where you play, so you can have a better idea. The diameter of the ring is 46 centimeters, the distance from the ring to the ring is 28/25 meters, the ball itself is 24 centimeters in diameter, the width of the court is 15 meters and the distance from the 3-point line to the ring is 5.8 meters.
Understand the essence of the throw. There are three factors involved when a player throws the ball: angles, push, and hand position. A large angle must be applied (understanding the angle as a perpendicular line from the hips and extension of the arms). It is possible to shoot higher when there is a defender in front, it is also recommended to shoot at an angle of 45 degrees or more, as this helps to get the ball into the basket softer and cleaner. The elbow should be as close to the face as possible to keep the ball in a straight line.![]() It is recommended to stretch your hand as far as possible, this increases the power of the throw.
It is recommended to stretch your hand as far as possible, this increases the power of the throw.
Recognize the math in bouncing off the floor. The ball is a hemisphere that will have a reverse effect depending on the force that was applied to it. When the ball is poorly inflated, it will not bounce as well as when it is full of air, the same is true when a player hits the ball incorrectly. You need to apply a certain amount of force to the ball, depending on if you want to give a confident long pass, if you are running or if you are dribbling. You need to use a more direct angle with strong passes, if you need to throw further, and when running, keep the ball at hip height, so speed is maintained.
Understand the trajectory of throws. The parabola is a curved line that you get with every throw. When throwing, you need to understand that the higher the parabola, the cleaner or easier the ball flies into the basket, and the lower, the more likely it is that the ball will hit the bow.![]() For the full effect of the parabola, it is necessary to apply " completion " with the wrist, which means that the player must give the ball a spin effect at the end of the throw using the hand.
For the full effect of the parabola, it is necessary to apply " completion " with the wrist, which means that the player must give the ball a spin effect at the end of the throw using the hand.
Thus, during the work on the project on the topic "Mathematics and Sports" we came to the conclusion that the use of mathematics and geometry has a positive effect on the results in basketball.
By understanding the percentage of completed and failed rolls, one can strive to improve efficiency.
The ball flies along a given trajectory. Selecting the correct geometry results in an efficient completion of a shot or pass.
Also, intense training allows you to relax after mental activity in the learning process.
Changing the type of activity has a positive effect on school performance.
Conclusion
It is useful for fans of intellectual games to know that in sports and sports games intelligence, education, calculation are far from superfluous things.![]()
So, as a result of our work, we made the following conclusions:
sport is an intellectual occupation, practical mathematics helps to achieve high sports results.
our hypothesis was confirmed: if you apply the knowledge of mathematics correctly, you can achieve high results in basketball.
Sports competitions provide the researcher with the richest material; it is fixed by coaches, carefully preserved, constantly accumulated. There are ample opportunities for experimentation, testing of mathematical models and optimal strategies in sports situations.
Area: " mathematics and basketball " is rich in new interesting research and results.
In the future, I plan to study basketball theory, tactics, use of mathematics, geometry and physics in more depth to improve the efficiency of my game and the game of my team, and, of course, continue to study exact sciences in depth, read books of various genres,
Mikhail Vasilievich Lomonosov: Mathematics should be loved already because it puts the mind in order ".![]()