Home »
Misc »
How basketball relates to math
How basketball relates to math
Math in Basketball – How Math Is Used in Sports – Cool Math
At first glance, basketball and math seemingly have little in common. While basketball is hugely popular in American schools, math has a considerably smaller fan following. However, a closer look at the sport reveals that there is a considerable amount of math in basketball. Pointing out how math is used in basketball is a great way to get your kids more excited about angles and percentages, while helping them realize how important math is in everyday life.
The angle at which the ball is thrown is determined as the angle made by the extension of the player's arms and a perpendicular line starting from the player's hips.The math in basketball involves a wide range of math topics. Kids can practice geometry, percentages and even basic mathematical operations while playing or watching a game of basketball.
Whether they realize it or not, basketball players make use of many geometric concepts while playing a game.![]()
The most basic of these ideas is in the dimensions of the basketball court. The diameter of the hoop (18 in), the diameter of the ball (9.4 in), the width of the court (50 ft) and the length from the three point line to the hoop (19 ft) are all standard measures that must be adhered to in any basketball court. Knowing these measurements is useful for kids who would like to practice basketball at home without access to a full-fledged basketball court.
The path the basketball will take once it’s shot comes down to the angle at which it is shot, the force applied and the height of the player’s arms. When shooting from behind the free throw line, a smaller angle is necessary to get the ball through the hoop. However, when making a field throw, a larger angle is called for. When a defender is trying to block the shot, a higher shot is necessary. In this case, the elbows should be as close to the face as possible.
Understanding arcs will help determine how best to shoot the ball.
Basketball players understand that throwing the ball right at the basket will not help it go into the hoop. On the other hand, shooting the ball in an arc will increase its chances of falling through the hoop. Getting the arc right is important to ensure that the ball does not fall in the wrong place.
The best height to dribble can also be determined mathematically. When standing in one place, dribble from a lower height to maintain better control of the ball. When running, dribbling from the height of your hips will allow you to move faster. To pass the ball while dribbling, use straighter angles to pass the ball along a greater distance.
Understanding geometry is also important for good defense. This will help predict the player’s moves, and also determine how to face the player. Facing the player directly will give the player greater space to move on either side. However, facing the player at an angle will curb his freedom. Mathematics can also be used to decide how to stand while going on defense.
The more you bend your knees, the quicker you can move. Utilizing geometry, math in basketball plays a crucial role in the actual playing of the sport.
Statistics is essential for analyzing a game of basketball. For players, statistics can be used to determine individual strengths and weaknesses. For spectators, statistics is used to determine the value of players and analyze the performance of an individual or the entire team. Percentages are a common way of comparing players’ performances. It is used to get values like the rebound rate, which is the percentage of missed shots a player rebounds while on the court. Statistics is also used to rank a player based on the number of shots, steals and assists made during a game. Averages are used to get values like the points per game average, and ratios are used to get values like the turnover to assist ratio.
- Addition and Subtraction in Basketball
For young basketball fans, math in basketball is a great opportunity to practice simple skills like counting, addition and subtraction.
Young kids can add up the points made in every shot to get the team’s total score. Kids can also be asked to use subtraction to determine how many points a team will need to catch up with the leading team, or to win the game.
The math behind the perfect free throw
Some 20 years ago, my colleague Dr. Chau Tran and I developed a way to simulate the trajectories of millions of basketballs on the computer.
We went to the coaches and assistant coaches at North Carolina State University, where we are based, and told them we had this uncommon ability to study basketball shots very carefully.
Their first question was simple: “What’s the best free throw?” Should the shooter aim towards the front of the hoop or the back? Does it depend on whether the shooter is short or tall?
Math offers a unique perspective. It speeds up the amount of time it takes to see the patterns behind the best shots. For the most part, we discovered things that the players and coaches already knew – but every so often, we came across a new insight.
Simulating millions of shots
From a mathematical viewpoint, basketball is a game of trajectories. These trajectories are unique in that the ball’s motion doesn’t change much when it’s flying through the air, but then rapidly changes over milliseconds when the ball collides with the the hoop or the backboard.
To simulate millions of trajectories without the code taking too long to run, we tried any trick we could think of. We figured out how to go from modestly changing motion to rapidly changing motion, such as when the ball bounces on the rim or off the backboard. We learned how to turn large numbers of trajectories into statistical probabilities. We even created fictitious trajectories in which the ball magically passes through all of the physical obstacles (hoop, backboard, back plate) except for one, to see where it collides first.
How a mathematician sees a free throw. Larry Silverberg, CC BY-SA
The free throw was the first shot that my colleague and I studied in detail.
In close games, teams can win and lose at the free-throw line. What’s more, the free throw is uncontested, so perfection in the free throw can pay off big. Top teams tend to shoot the free shot well.
Our program could tell us what chances the shooter had in sinking a free throw – and help us figure out what he was doing right or wrong.
Breaking down the free throw
We studied the free throw for about five years.
One of the first things we learned from our simulations and by watching TV footage was that players with the same consistency can shoot free throws with anywhere from 75 to 90 percent accuracy. The difference was that the 90 percent players were being consistent at the right shot - the best trajectory.
The fate of a free throw is set the instant the ball leaves the player’s fingertips, so we looked closely at the “launch conditions” of the shot. The ball is located at some height above the floor. It has a rate at which it is spinning backwards (called backspin), and it has a launch speed and a launch angle.
Since the shooter never launches the ball the same way, small differences account for a shooter’s consistency.
We found that about 3 hertz of backspin is the best amount; more than that does not help. It takes about 1 second for a ball to reach the basket, so 3 hertz equates to three revolutions in the air, from the instant the ball leaves the player’s hands to when it reaches the basket.
Next, assuming the player releases the ball at 7 feet above the ground, a launch angle of about 52 degrees is best. In that angle, the launch speed is the lowest, and the probability of the shot being successful is the greatest. At 52 degrees, the shooter can be off a degree or more either way without a large effect on the shot’s success.
However, launch speed is quite the opposite. It’s the hardest variable for a player to control. Release the ball too slowly and the shot is short; release it too fast and the shot is long. A player needs to memorize the motion of her entire body during release to impart the same speed consistently.
All else being the same, players who release from higher above the floor have a higher shooting percentage. That’s interesting, because our coaches at N.C. State and others I have talked say that taller players tend to shoot the free throw worse than shorter players do. It seems that the shorter players must try harder.
The last release condition was the most surprising: the aim point of the free throw. We found that the player should aim the ball to the back of the rim. Basically, the back of the rim is more forgiving than the front of the rim. At a release height of 7 feet, the gap between the ball and the back of the ring should be less than 2 inches. A small gap is best whether launching at low or high release heights.
Lessons learned
So what does this all mean for players out there aspiring to improve their free throw?
Our research suggests that players should aim the ball beyond the center of the rim. Launch the ball at a high angle and as high above the ground as possible.
(The ball, at the highest point of its arc, should reach the top of the backboard.) Line up the ball to eliminate the side angle. And try to launch the ball with smooth body motion, to produce a consistent launch speed.
In the past few years, we’ve expanded our work to study where the best bank shots strike the backboard and developed a tool for anyone who wants to perfect it.
With tournament play underway, I’m reminded of how competitive the game has become, and how it has truly become a game of inches. As an old basketball player, like many of you, I enjoy watching the game – and, every so often, catching a glimpse of that perfect free throw.
Research project of 7th grade students on the topic "Mathematics in Basketball"
Ministry general and vocational education
Sverdlovsk regions
Municipal autonomous educational institution -
secondary secondary school No. 91
in-depth study of individual subjects
MO City of Yekaterinburg
Chkalovsky district
Name sections (subsections): natural sciences (mathematics)
Research job: Mathematics in basketball
Author(s) of the job: Korshunov Maxim Alexandrovich , 7th grade
Khamidulin Andrey Sergeevich , 7th grade
Head (supervisors) of work: Grishina Anna Aleksandrovna ,
teacher Mathematics and Informatics
____________________
____________________
2020
Contents
Introduction.
3
Chapter 1 Mathematics and basketball. 5
1.1. Basketball game. 5
1.2. Game features. 6
Chapter 2.9
2.1. Location of players on the field. 9
2.2. Calculation of dependencies. 10
Conclusion. 15
List literature: 16
Application 1. The first rules of the game. 17
Application 2. Game basketball field. 19
Application 3. Questionnaire for 7th grade students. 20
Application 4. Survey results. 21
Application 5. Screenshot of the report of the results of checking the project file by the " Anti-plagiarism " system. 22
Mathematics is a science that studies numbers, quantitative relations and spatial forms. Mathematics is a subject that studies this science. We often hear and see such definitions. For us, mathematics is a way of describing various phenomena of nature and especially society. Since in Mathematics acts as an assistant in all spheres of human activity.
For example, performing calculations when creating machines, exploring space, even creating literary works and that requires mathematics.
We were interested in the question “Sport. Can mathematics to help this area of human activity with precise and strict language? Of course, the very first answer is chess.
But, we decided to check out other sports as well. Since we are already we have been playing basketball for several years, then our choice fell on this particular type sports.
The topic of our research is “Mathematics in Basketball”.
Purpose of research : to study the influence of mathematics on basketball, to calculate the mathematical model of the best game with the maximum number of hits.
Tasks :
1. To study the literature on the research topic;
2. Compare and contrast common terms and concepts in mathematics and basketball;
3. Analyze the results obtained;
4. Show the application of the acquired knowledge in basketball;
Hypothesis: is it possible to build a mathematical model of an ideal basketball game.
Object research: mathematics and basketball.
Item research: mathematical component in basketball.
the following methods were selected : study of literary sources, processing of the received information, analysis, synthesis, research, practical.
Product project : creation of a mathematical model of the best game with the maximum the number of hits.
Practical significance : results can be use in additional education and self-education.
Basketball (basket - basket, boll - ball) is team game in which players throw the ball into the "basket", consisting of a ring with a mesh at the bottom. It is located at a height of just over 3 meters. from the floor (10 feet), to be more precise 3.05m. Picture 1
Dr. James is considered to be the founder of the game Naismith, who decided to diversify gymnastics lessons at the training center Christian Youth Association in Springfield, Massachusetts (USA) 1891.
His idea was to throw a soccer ball in two fruit baskets without a bottom, which he attached to the balcony railing. Fans on the balconies they caught flying balls and tried to throw them into the opponent's basket, therefore, shields appeared that became the protection of the basket, and in 1893 appeared already iron rings with mesh. Given the shortcomings of the first matches, D. Naismith in during the year develops the first 13 points of the basketball rules (Appendix one).
The new game was so addictive that in 1894 The first official rules were issued in the USA. Within 10 years basketball begins to "capture the world", first the East - Japan, China, the Philippines, and then the game comes to Europe, South America, the end of this journey becomes the Olympic Games in St. Louis (USA), where the Americans organized demonstration tournament between teams from several cities. Basketball was indicative also at the 1924, 1928 Olympics.
In 1923 France hosts the first international women's tournament, in which countries participated: England, Italy, USA.
The game is gaining more and more popularity and recognition in the world, and at 1932g. was The International Basketball Federation (FIBA) was founded. The first composition of the federation included 8 countries - Argentina, Greece, Italy, Latvia, Portugal, Romania, Sweden, Czechoslovakia. In 1935, the International Olympic Committee decided to recognition of basketball as an Olympic sport. In 1936 at the Olympic Games in Berlin in the program appeared basketball. D. Naismith was the guest of honor of the games - creator of this game. Teams from 21 countries participated in the basketball tournament.
Basketball comes to Russia at 1906g, to the city - Petersburg, in the sports society "Mayak" and before the October Revolution 1917 remains the game only of this city. Actively play basketball throughout country begins after 1923, and the WTO began to participate in world championships from 1959
The game does not have one main technique, it includes various game techniques and performance variations.
chief the rule for the player is: accessibility, rationality of actions together with purposefulness, jumps are accurate and fast, giving the player maneuverability on field.
There are two teams of 12 people. There are 5 players from each team on the playing field. Goal: to score bigger opponent's ring the number of balls to prevent the second team from grabbing the ball and scoring into their own ring. Depending on the where the player throwing into the ring is located, a different number of points are counted for hitting. For a free throw 1 point is counted, for a throw from an average or close distance (in the jargon - paint) - 2, and 3 points given for a throw from behind the 3-point line. (Annex 2)
The ball is played with the hands only. Prohibited: running with the ball in your hands without hitting it on the floor, deliberately hitting it fist or leg, block with any part legs. Accidental touches with the foot or leg are not violations of the rules of the game. The beginning of the game is considered controversial throw in the central circle of the field, two players from rival teams.
The match is divided into four periods 10 minutes each (12 minutes in the NBA). Between the 2nd and 3rd quarters of the game is regulated break 15 minutes, other pauses are two minutes each, and in addition, coaches (in the NBA - and players) can take timeouts. After half the game, the teams must swap halves of the field.
The winner is the team that during the game was able to score more points. In case of a tie after the end of the regular time of the game, overtime is assigned, usually this is additional five minutes of play if given there is not enough time, the second, the third is assigned ... until one of the teams scores more points, and there is no the winning team is declared.
In order for the game to be effective and not like a chaotic movement around the field, roles assigned to players:
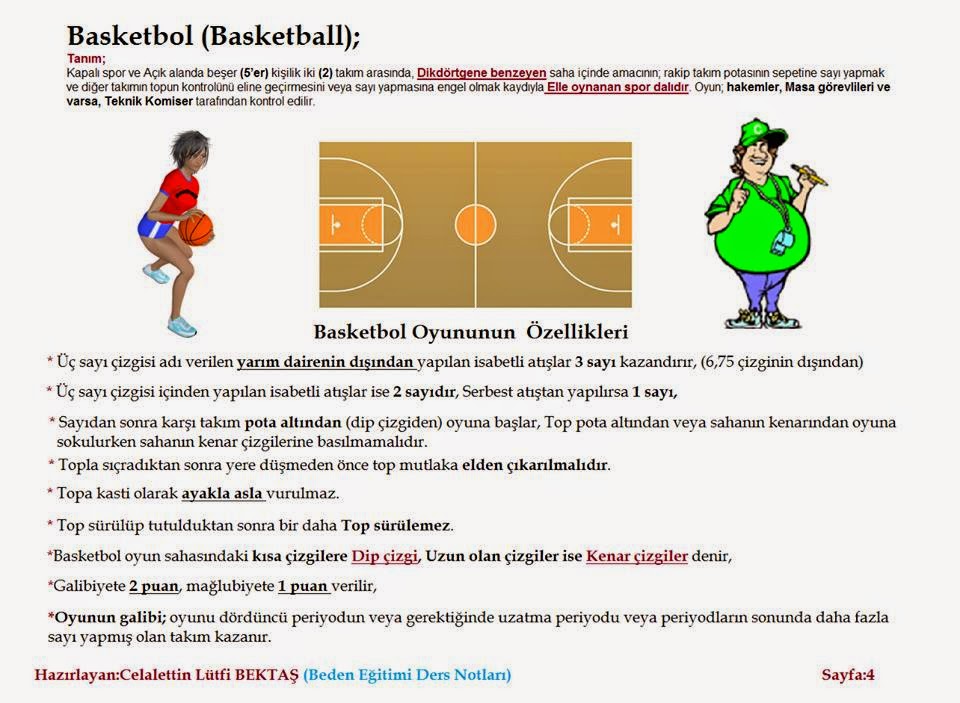
- point guard point guard or playmaker (eng. Play maker) - number one team responsible for choosing the combination of the game, which way to go and how build an attack.
This player not only needs to see teammates, but also calculate the situation on the site.
- attacks - perfect possession of the ball and movements;
- protection - possesses the skills of tackling the ball. The main goal of such a player is to insure team from a fast break of the opposing team.
Such division was in the past. In the modern professional basketball, priority is given to versatile players who combine the qualities which allow the player to play adjacent positions. This is how the position stands out comboguard (eng. Combo Guard). Based on the name, it can be determined that the player combines a combination of qualities necessary for defense and attack.
It is possible to classify players not only by type of activity on court, but also by height and weight:
- Average height 183-195 centimeters, weight 75-90 kilograms - this is point guard defender (eng. Point guard) or playmaker (eng. Play maker).
- Player average height 190-200 centimeters, weight 85-100 kilograms - attacking defender (eng.
Shooting guard).
- Average height 195-210 centimeters, weight 95-110 kilograms - light forward (English Small Forward).
- The average height of a professional player is 200-215 centimeters, weight 105-115 kilograms - heavy forward (English Power Forward)
-Average height 210-220 centimeters, weight 110-125 kilograms - center (English Center).
Analyzing the game after training or a match often, you ask yourself: “Is it possible to improve your results or how to come up with the ideal model for the game and always score the maximum number of points?
To find answers to these questions, we decided to turn to our peers, but before that find out “How many of them know about this game generally?". For this purpose, a survey was conducted among 7th graders. (Annex 3)
As a result, we find that only 80% of the respondents know such a game, and about the rules and features in general, only 50%. Analyzing all this, we there was an idea to create a mathematical model of an ideal game, which means to solve the following tasks:
1.
Reviewed various positions of the player on the field.
2. Formulas studied depending on the distance between the player and the basket.
3.According to with these formulas, the positions of the players of the school team were calculated.
4.Checked practical way these results.
Drawing 2
Depending on the position of the players located on the field in certain areas where they can best be implemented in accordance with their classification. Looking at the positions we investigated and got such a picture (Figure 2).
When a player "fouls" during a shot, then he gets on the penalty (in the figure - the yellow line) line and throws as many times he could score points on the throw - 1 point. Zone in which any goal will be counted as two points, shown in red in the figure. Purple zone - this is the zone in which any goal will be counted for 3 points. This is the location of the zones for the left ring.
Basketball - dynamics, movement speed and quickness. In addition, this competent execution of throws. At the same time, you need to know how to properly fulfill. Let's try to figure out how to throw the ball, under what angle and at what speed to hit the basket when throwing from different distances.
On average, a player makes about 20 shots from different distances and that the game is of high quality, and the player showed good results, he needs to distribute his forces throughout the game, without putting in too much effort. But the player not only throws the ball, but also overcomes the barrier in the form of a defender, for this the ball must be thrown through it and get into the basket. It is clear that the closer the defender is to me, then the higher the trajectory of the ball will be required, and then this is subject to constant hit. But people with 100% accuracy very rarely meet m, then additional calculations are needed.
Let's introduce some designations and consider their data:
1.
D M is the diameter basketball ball. A standard basketball has a diameter of 24 cm.
2. m is the mass of the ball. In the standard is 600 g.
3.H - height hoops of a basketball hoop above floor level. In standard gyms - 3.05m.
4. D K - ring diameter, it is equal to 45 cm.
5. L - distance from the center of the ring to the place of the throw.
Figure 3
during the calculations, we will consider basketball ball with a material point, while neglecting the influence of air on the flight of the ball. Let's choose a system coordinates yOx to describe the movement: axis Ox - directed horizontally, the Oy axis is directed vertically, the origin of the coordinate system O coincides with the center of the ball at the start of the throw. Since the ball is moving with free acceleration fall g=9,8m/s 2 , directed vertically down, then using kinematic equations of motion we obtain:
, where v 0 x is the horizontal projection of initial ball velocity, v 0 y – vertical projection of initial velocity ball.
After mathematical transformations, we obtain the trajectory equation ball: , where α is the angle between the direction of the initial speed v 0 and the positive direction of the 0x axis, and the tangent of the angle α is:
, where β is the angle at which the ball flies into the basket.
After transformations of the equations, we obtain a formula for determining the initial velocity ball:
Performing calculations to find the initial speed at different throwing angles for different areas of the field (different types of points), we were several best angles are marked (Table 1). At the same time, in calculations, the growth the player was taken into account as the average height for our school basketball team 1.71 m. The flight path L changed depending on the location of the player along zones on the site, the angle α varied from 20 0 to 90 0 .
Table 1
| No. | υ 0 m/s | h, m | L, m | α |
| Single point zone |
| 1 | 5.61 | 1.71 | 4.3 | 30 0 |
| 2 | 4.8 | 1.71 | 4.3 | 45 0 |
| 3 | 4.1 | 1. 71 | 4.3 | 60 0 |
| Two-Point Direct Zone |
| 4 | 6.5 | 1.71 | 5.8 | 30 0 |
| 5 | 5.4 | 1.71 | 5.8 | 45 0 |
| 6 | 4.5 | 1.71 | 5.8 | 60 0 |
| Two-point side zone |
| 7 | 5.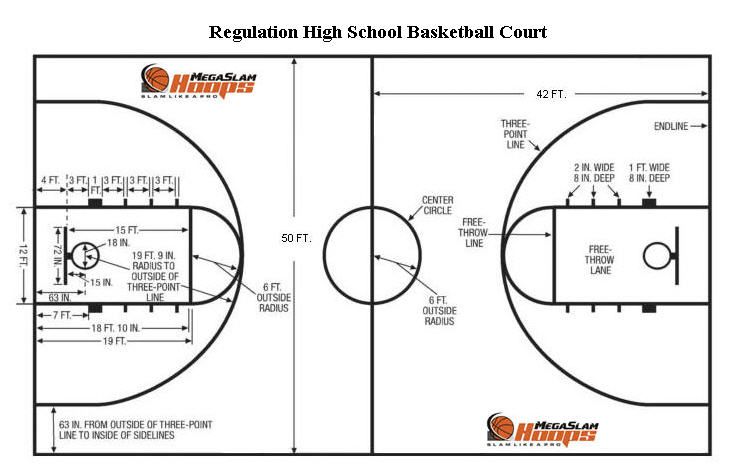 6 | 1.71 | 4.35 | 30 0 |
| 8 | 4.8 | 1.71 | 4.35 | 45 0 |
| 9 | 4.1 | 1.71 | 4.35 | 60 0 |
| Three-Point Direct Zone |
| 10 | 6.9 | 1.71 | 6.48 | 30 0 |
| 11 | 5. 7 | 1.71 | 6.48 | 45 0 |
| 12 | 4.7 | 1.71 | 6.48 | 60 0 |
| Three-point side zone |
| 13 | 7.5 | 1.71 | 7.55 | 30 0 |
| 14 | 6.1 | 1.71 | 7.55 | 45 0 |
| 15 | 5 | 1. 71 | 7.55 | 60 0 |
The selection of these corners is also related to the coverage area of the ring:
1. If the ball is thrown at an angle of 60° to the plane of the basket, then only 0.8661 parts of the ring are used.
2.If throw taken at a 45° angle, the target is 0.7071 rings.
3. When thrown under an angle of 30 °, the affected area is reduced to 0.5 rings.
Received the data helped us determine the ideal muzzle velocity for a given angle and flight path length.
Another factor affecting the flight of the ball is rotation ball. According to the rules, the ball must be thrown with reverse rotation. This is necessary in order to to keep the ball in its flight path, increasing the chances of hitting basket, by slowing down the speed of the ball. But it's all physical phenomena that we will not count.
As a result of calculations conclusions can be drawn:
- the smaller the angle throw, the smaller the chances of getting the ball into the basket, which means there should be increased accuracy.
This can be achieved by increasing the height of the flight path.
- the higher flight path, the longer the flight path of the ball.
- first case ideal and almost never found in sports, but the most acceptable throw angle ball 60 0 .
- attached at throw force determines the initial speed of the ball, which in turn determines the height of the ball's flight path. If you apply maximum force, then the accuracy will drop.
After analyzing all the results, we decided to check them on practice. Throwing the ball was carried out in accordance with the length of the trajectory flight and angle of inclination, which we first measured with a protractor. (Picture 4) In each of the cases, the hit was accurate, which means our calculations are confirmed.
Figure 4
6 30
0 ) (angle 60
0 )
affecting the quality of the throw, for example, physical and psychological.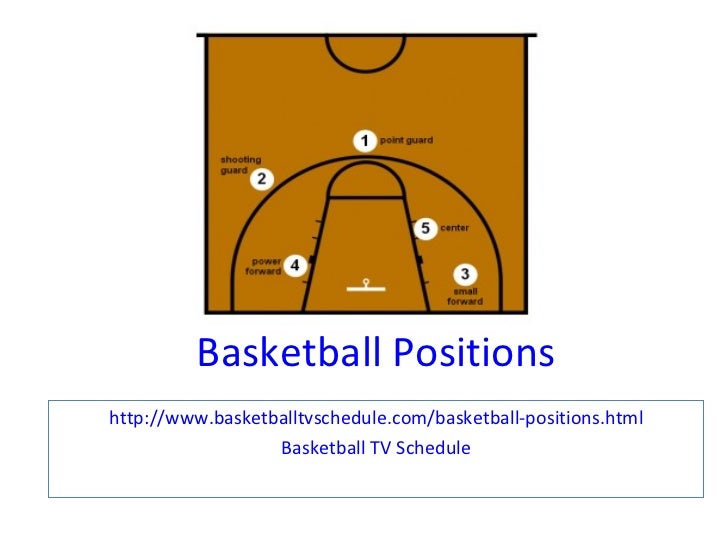
As well as in our calculations, we did not take into account physical phenomena and their calculations, which will be studied by us in the future in the course "Physics" and then our formulas and calculations will be finalized.
Working on this topic, we confirmed our hypothesis: it is possible whether to build a mathematical model of an ideal basketball game. But would like add that this is possible when taking into account a large number of factors - rotation ball, flight path, player height, etc.
In conclusion, we add that basketball is not only a beautiful sight sports, but the connection of physics and mathematics, where mathematics is an assistant.
For us, this project was the starting point in the study of only mathematics, physics, but in the awareness of the vast field of application of mathematics to human activity, and as Alfred said North Whitehead: "The most interesting property arithmetic is that it applies to everything: to taste sensations and sounds, to apples and angels, to thoughts and bones.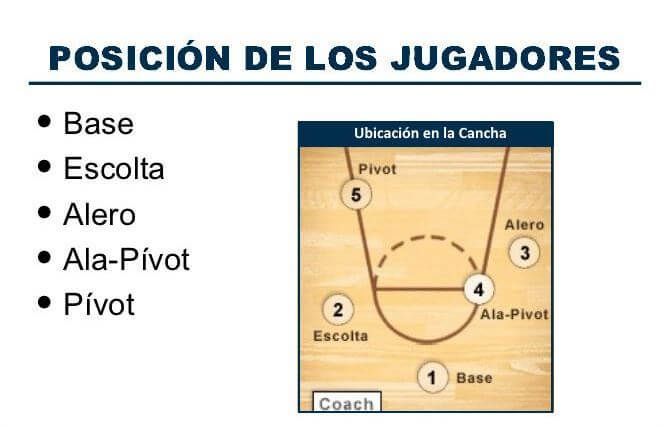
”
1. Gershenzon EAT. Mechanics: Proc. Allowance for students. Higher pedagogical educational institutions / E.M. Gershenzon, N.N. Malov, A.N. Mansurov. - M .: Publishing Center "Academy", 200. - 384 p.
2. Pichurin L. F. Za pages of the textbook of algebra: book. for students in grades 7–9 avg. school - M .: Enlightenment, 1990.– 224 p.: ill.
3.http://sdushortambov.ru/index.php?option=com_content&task=view&id=73&Itemid=1
4.https://vm.ru/sport/163491-13-pravil-basketbola-dzhejmsa-nejsmita
5.https://sportyfi.ru/basketbol/priemi/peremeshchenie/
-o-pravilah.html
7.http://life.mosmetod.ru/index.php/item/kak-zabrosit-myach-v-basketbolnuyu-korzinu
8.http://images.yandex.ru
9.https://www.nkj.ru/archive/articles/33854/
1. The ball can be thrown in any direction with one hand (now you can throw with two hands).
2. You can hit the ball hit with one or two hands in any direction, but never with a fist (this hasn't changed, but accidental touches don't count).
3. The player cannot run with the ball. The player must throw the ball from the point at which he caught it, an exception is made for a player running at high speed (now with the ball you can run).
4. Ball needed keep brushes. You can not use the forearms and body to hold the ball.
5. In any case hitting, grabbing, holding and pushing the opponent are not allowed. First violation of this rule by any player shall be called a foul; second foul disqualifies him until the next ball has been potted, and if any the obvious intention to injure the player is a disqualification for the entire game. At it is not allowed to replace a disqualified player. (now allowed 5 fouls with removal to the bench and replacement of the player).
6. Hitting the ball fist - violation of paragraphs of rules 2 and 4, the punishment is described in paragraph 5.
7. If any of side commits three fouls in a row, then a goal is recorded for its opponent (this means that during this time the opponent must not commit a single foul).
8. Goal counts if a ball thrown or bouncing off the floor enters the basket and stays there. Defending players are not allowed to touch the ball or basket in throw moment. If the ball touches the edge and the opponents move the basket, then a goal is counted (now the ball bouncing off the floor does not bring points to the team, but the ball can be helped in flight).
9. If the ball goes out of bounds, he must be thrown into the field by the first to touch his player. In the event of a dispute, the referee must throw the ball into the field. thrower the player is allowed to hold the ball for five seconds. If he keeps it longer, then the ball is given to the opponent (nowadays, if the team is delaying time, they are given foul).
10. The referee must monitor the actions of players and fouls, as well as notify the referee of three fouls committed in a row. He is vested with the power to disqualify players according to rule 5.
11. The referee must watch the ball and determine when the ball is in play (inbounds) and when going into touch (out of bounds), which side shall be in possession the ball, as well as perform any other action that is normally performed by the referee (Now the referee can help the side judge).
12. The game consists of two halves of 15 minutes each with a break of 5 minutes between them (now four games of ten minutes each. First and last break - two minutes, between halves - 15 minutes).
13. Party, scoring more balls during this period of time is the winner.
Middle Logical Thinking
DISCULATION and Development of Mathematics abilities of rural children. Development logical thinking.
The work of the camp is an integral part teaching and educational process of education. AT our camp is working on development mathematical abilities of students in extracurricular time as a continuation of the academic process. We are working on the development of creativity thinking of students, since the ability to independently think, make theoretical generalizations, acquire knowledge, navigate freely the flow of scientific information is paramount meaning.
Theoretical thinking is not independent and isolated mental process. Therefore, when planning classes in teacher camp pays great attention development of logical thinking, ingenuity, imagination, flexibility of thinking, development mechanical and logical memory using special exercises and games.
Forms and methods of teaching in summer math camp must match age abilities of students. Based of this, mathematical games are held: matboy, quizzes, intellectual marathon, “What, Where, When?”, mathematical lotto.
To form a sustainable interest in mathematics requires not only mathematical games and entertaining tasks, considerations sobrisms, solving puzzles, but also problematic presentation, hypotheses, consideration of various ways of solving problems, proof of theorems by various methods and performances of the students in the classroom.
To improve cognitive, creative the activity of students is of great importance work and protection of abstracts.
Work on the abstract includes recommendations for topic selection, ongoing consultations, verification and individual interviews.
Students choose topics for essays themselves, for example:
- “Fractions in Rus'”,
- “From the history of zero”,
- “What is a broken number”,
- “How to write down the proportion
- “Geometric progressions in antiquity”,
- Fun Math Hour,
- “Essay “Geometry Lesson”,
- Match Games,
- “Disappearing figures”, etc.
Visual aids were made (Table math games). For seven seasons it was 41 games were made. For example: "The wolf and the sheep", “Numerical pyramid”, “Suvorov problem”, “Mill”, “Game 15”, “Game tactical “Focus”, “Labyrinth”, “Puzzle KIT”, “Magic Circle”, “Cage Route”, etc. Semenov Styopa's essay written during summer math camp led by Unarova L. A. Teachers of the highest category, excellent student of public education on the topic “Seven measure once, cut once” (Geometry of scissors).
FROM delivered this essay at the Republican teachers' seminar. In the city of Yakutsk 1996 year. Per good essay was invited in the summer mathematical camp in Yakutsk.
Theme "Euler circles"
Educational goals: The topic is closely related with set algebra. Application of Euler circles gives the problems of set algebra visibility and simplicity. Euler circles are successfully applied also in logical problems for the image truth sets of propositions and in many other cases. Image of task conditions in the form of Euler circles, as a rule, simplifies and makes it easier to reach a solution. This topic definitely broadens my mathematical horizons students enriches the arsenal of means, used in solving various problems.
Historical data:
Leonhard Euler for his long life (1707-1782) wrote more than 850 scientific papers. In one of them and these Euler circles appeared. He wrote then that “they are very suitable for facilitating our thoughts.
"
Problem 1. Count the mathematicians.
There are 35 students in the class. Of these, 20 are engaged in mathematical circle, 11 - biological circle, 10 guys do not attend these circles. How many biologists fond of math?
DISCUSSION.
Draw these circles on a large circle - school yard. We place all mathematicians in the left circle and denoted by the letter M., and in the right all biologists and denoted by the letter B. In the common part of the circles will be the same biologists and mathematicians who interested. The remaining 10 will be asked not to enter from the outer circle, the largest. Now let's count 35 guys inside the big circle, inside two smaller 35 - 10 + 25 inside "mathematical" circle M is 20 guys, means, in that part of the “biological” circle, which is located outside the circle of M., is 25-20 \u003d 5 biologists who do not attend the mathematical circle. The remaining biologists, there are 11-5+6 of them, are in common part of MB circles.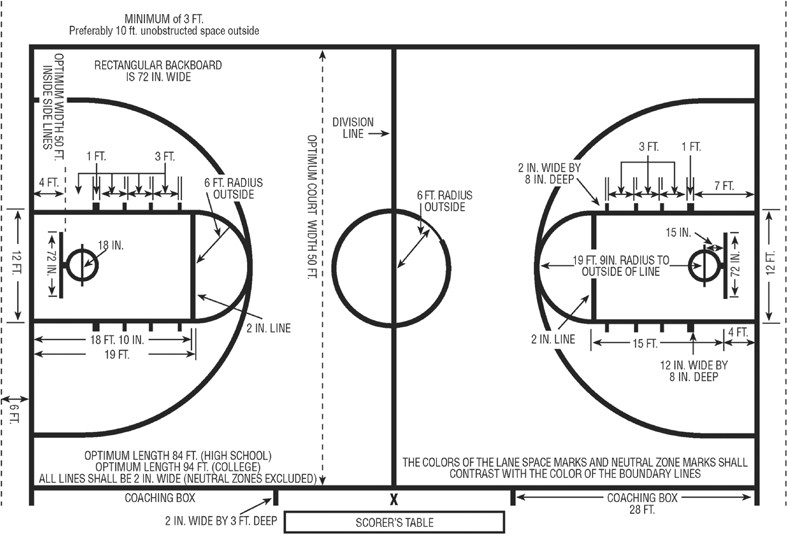
So 6 biologists fond of mathematics.
Questions to check:
- math circle and as shown in drawing?
- How many guys attend only one circle?
Task 2.
There are 38 people in the class. Of these, 16 in basketball, 17 in hockey, 18 - volleyball. Involved in two types sports - basketball and hockey - four, basketball and volleyball - three, volleyball and hockey - five. Three are not addicted neither basketball, hockey or volleyball.
A. How many guys are not addicted at the same time three sports?
B. How many guys are addicted to only one of these sport?
DISCUSSION.
Let's use the Euler circles. Many of all Let's draw the students of the class as a large circle (Fig. 2)
Inside which we will place three smaller circles. Designation: B - basketball players, X - hockey players, B - volleyball players.
Number of elements of the BHV set through u. From an examination of the Euler circles, it can be seen that the numbers of BHV, BHV and BHV elements are equal respectively
16-(4+y+3)=9-y, 8-y and 10-y 38= 3+(9-y)+(8-y)+(10-y)-4+3+5 +y from here Y=2
three sports. Adding Quantity elements of disjoint sets, number BHV, BHV and BHV elements i.e. 9-2=7, 8-2=6, 10-2=8, 7+6+8=21 - addicted to one of these sports.
Subject: Euler circles
- There are 35 students in the class. Of these, 20 are engaged in mathematical circle, 11 - biological, 10 children do not attend these circles. How many biologists fond of math?
- There are 38 people in the class. Of these, 16 play basketball, 17 in hockey, 18 in volleyball. Interested in 2 sports basketball and hockey 4, basketball and volleyball 3, volleyball and hockey 5. Three are not fond of either basketball, volleyball, or hockey. How children are fond of three types at the same time sports?
- There are 40 students in the class.
:no_upscale()/cdn.vox-cdn.com/uploads/chorus_asset/file/13128999/KELDON_JOHNSON_MBB2018_01_CW_600x900.jpg)
